Sinus und Kosinus

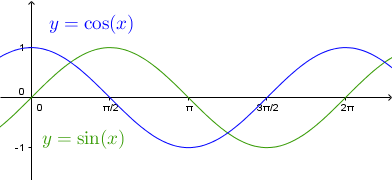
sincos.png
Graphen der Sinusfunktion (grün) und der Kosinusfunktion (blau). Beide Funktionen sind 2π2 \pi -periodisch und nehmen Werte von −1-1 bis 11 an.
Die Sinus- und Kosinusfunktion (auch Cosinusfunktion) sind trigonometrische Funktionen. Sie werden unter anderem in der Geometrie für Dreiecksberechnungen und in der Analysis benötigt.

Geometrische Definition

Definition am rechtwinkligen Dreieck

Die Längenverhältnisse der drei Seiten im rechtwinkligen Dreieck sind nur abhängig vom Maß der beiden spitzen Winkel. Da aber das Maß eines dieser Winkel das Maß des anderen Winkels bereits festlegt (die Winkelsumme der beiden spitzen Winkel im rechtwinkligen Dreieck beträgt stets 90°90°), hängen die Längenverhältnisse im rechtwinkligen Dreieck nur vom Maß eines der beiden spitzen Winkel ab.
 
 
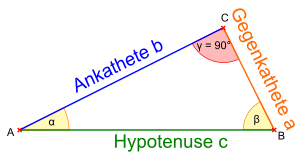
RechtwinkligesDreieck.png
Abb. FO99: Dreieck mit einem rechten Winkel in CC. (Benennung von An- und Gegenkathete unter der Annahme, dass α\alpha der betrachtete Winkel ist.)
Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel).
Sinus eines Winkels\text{Sinus eines Winkels} =Gegenkathete des WinkelsHypotenuse= \frac{\text{Gegenkathete des Winkels}}{\text{Hypotenuse}}
Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.
Kosinus eines Winkels\text{Kosinus eines Winkels} =Ankathete des WinkelsHypotenuse= \frac{\text{Ankathete des Winkels}}{\text{Hypotenuse}}
Bei den für Dreiecke üblichen Bezeichnungen der Größen (siehe Abb. FO99) gilt hier:
sin⁡(α)=ac\sin (\alpha) = \frac{a}{c} \quad und cos⁡(α)=bc\quad \cos (\alpha) = \frac{b}{c}.
Da die Hypotenuse die längste Seite eines Dreiecks bezeichnet, gelten die Ungleichungen sin⁡(α)≤1\sin\left(\alpha\right)\leq 1 und cos⁡(α)≤1\cos\left(\alpha\right)\leq 1.
Wird statt von α\alpha von dem gegenüberliegenden Winkel β\beta ausgegangen, so wechseln beide Katheten ihre Rolle, die Ankathete von α\alpha wird zur Gegenkathete von β\beta und die Gegenkathete von α\alpha bildet nun die Ankathete von β\beta und es gilt
sin⁡(β)=bc\sin (\beta) = \frac{b}{c}\quad und cos⁡(β)=ac\quad \cos (\beta) = \frac{a}{c}
Da im rechtwinkligen Dreieck α+β=90∘\alpha + \beta = 90^\circ gilt, folgt
cos⁡(α)=sin⁡(90∘−α)=sin⁡(β)\cos (\alpha) = \sin(90^\circ - \alpha) = \sin(\beta)
und
sin⁡(α)=cos⁡(90∘−α)=cos⁡(β)\sin (\alpha) = \cos(90^\circ - \alpha) = \cos(\beta).
Aus dem Satz des Pythagoras lässt sich die Beziehung ("trigonometrischer Pythagoras") ableiten:

Satz 5220B

sin⁡2(α)+cos⁡2(α)=1\sin^2 \left(\alpha\right) + \cos^2 \left(\alpha\right) = 1.

Definition am Einheitskreis

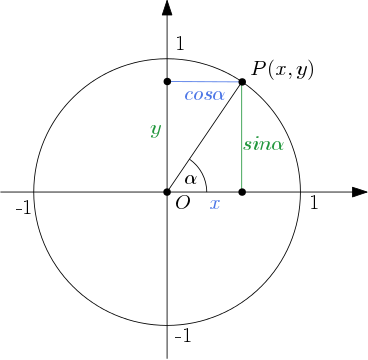
SincosEk.png
Definition am Einheitskreis.
Im rechtwinkligen Dreieck ist der Winkel zwischen Hypotenuse und Kathete nur für Werte von 00 bis 9090 Grad definiert. Für eine allgemeine Definition wird ein Punkt PP mit den Koordinaten (x,y)(x,y) auf dem Einheitskreis betrachtet, hier gilt x2+y2=1x^2+y^2=1. Der Ortsvektor von PP schließt mit der xx-Achse einen Winkel α\alpha ein. Der Koordinatenursprung (0,0)(0,0), der Punkt (x,0)(x,0) auf der xx-Achse und der Punkt P(x,y)P(x,y) bilden ein rechtwinkliges Dreieck. Die Länge der Hypotenuse beträgt x2+y2=1\sqrt{x^2+y^2}=1. Die Ankathete des Winkels α\alpha bezeichnet die Strecke zwischen (0,0)(0,0) und (x,0)(x,0) und hat die Länge xx, es gilt also cos⁡(α)=x\cos(\alpha)=x. Die Gegenkathete des Winkels α\alpha ist die Strecke zwischen (x,0)(x,0) und (x,y)(x,y) und hat die Länge yy, es gilt also sin⁡(α)=y\sin(\alpha)=y.
Diese Definition lässt sich auf andere Quadranten fortsetzen: Die yy-Koordinate eines Punktes des Einheitskreises entspricht also dem Sinus des Winkels zwischen seinem Ortsvektor und der xx-Achse, während die xx-Koordinate dem Kosinus des Winkels entspricht.

Analytische Definition

Definition durch Taylorreihen

Durch den Übergang vom Winkelmaß zum Bogenmaß können Sinus und Cosinus als Funktionen von R\R nach R\R erklärt werden. Die Taylorreihen stellen der Funktionen sin⁡(x)\sin(x) und cos⁡(x)\cos(x) sind:
sin⁡(x)=∑n=0∞(−1)nx2n+1(2n+1)!=x1!−x33!+x55!∓⋯\sin (x) = \sum_{n=0}^\infty (-1)^n\frac{x^{2n+1}}{(2n+1)!} = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}\mp\dotsb
cos⁡(x)=∑n=0∞(−1)nx2n(2n)!=x00!−x22!+x44!∓⋯\cos (x) = \sum_{n=0}^\infty (-1)^n\frac{x^{2n}}{(2n)!} = \frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}\mp\dotsb

Definition als Lösung einer Funktionalgleichung

Ein anderer analytischer Zugang ist, Sinus und Kosinus als Lösung einer Funktionalgleichung zu definieren, die im Wesentlichen aus den Additionstheoremen besteht: Gesucht ist ein Paar stetiger Funktionen sin⁡,cos⁡ ⁣:R→R\sin, \cos\colon\R\to\R, das für alle x,y∈Rx,y\in\R die Gleichungen
sin⁡(x+y)=sin⁡(x)cos⁡(y)+cos⁡(x)sin⁡(y) ⁣\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)\!
und
cos⁡(x+y)=cos⁡(x)cos⁡(y)−sin⁡(x)sin⁡(y) ⁣\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)\!
erfüllt. Die Lösung sin⁡\sin definiert dann den Sinus, die Lösung cos⁡\cos den Kosinus. Um Eindeutigkeit zu erreichen, sind einige Zusatzbedingungen zu erfüllen: sin⁡(x) ⁣\sin(x)\! ist eine ungerade Funktion, cos⁡(x) ⁣\cos(x)\! eine gerade Funktion, lim⁡x→0sin⁡(x)x=1\lim_{x\to 0}\frac{\sin(x)}{x}=1 und cos⁡(0)=1 ⁣\cos(0)=1\!.

Produktentwicklung

sin⁡(x)=x∏k=1∞(1−x2k2π2) \sin(x) = x \prod_{k=1}^\infty \left( 1 - \frac{x^2}{k^2\pi^2} \right)
cos⁡(x)=∏k=1∞(1−4x2(2k−1)2π2) \cos(x) = \prod_{k=1}^\infty \left( 1 - \frac{4x^2}{(2k-1)^2\pi^2} \right)
x  x\; ist dabei im Bogenmaß anzugeben.

Wertebereich und spezielle Funktionswerte

Zusammenhang zwischen Sinus und Kosinus

sin⁡(α)=−cos⁡(α+90∘)=cos⁡(α−90∘)\sin(\alpha)=-\cos\left(\alpha + 90^\circ \right)=\cos\left(\alpha-90^\circ\right) (Gradmaß)
sin⁡(α)=−cos⁡(α+π/2)=cos⁡(α−π/2)\sin(\alpha)=-\cos\left(\alpha + \pi/2 \right)=\cos\left(\alpha - \pi/2\right) (Bogenmaß)
Insbesondere folgt daraus ∣sin⁡α∣≤1|{\sin\alpha}|\leq 1 und ∣cos⁡α∣≤1|{\cos\alpha}|\leq 1.

Wichtige Funktionswerte

Da Sinus und Kosinus periodische Funktionen mit der Periode 2π2 \pi (entspricht im Gradmaß 360∘360^\circ) sind, reicht es, die Funktionswerte der beiden trigonometrischen Funktionen für den Bereich [0,2π][0,2\pi] (entspricht dem Bereich 0∘0^\circ bis 360∘360^\circ) zu kennen. Funktionswerte außerhalb dieses Bereichs können also aufgrund der Periodizität durch den Zusammenhang
sin⁡(x)=sin⁡(x+2kπ)undcos⁡(x)=cos⁡(x+2kπ)\sin(x) = \sin(x + 2k \pi)\quad \text{und}\quad \cos(x) = \cos(x + 2k \pi)
bestimmt werden. In Gradmaß lautet der Zusammenhang analog
sin⁡(x)=sin⁡(x+k⋅360∘)undcos⁡(x)=cos⁡(x+k⋅360∘) .\sin(x) = \sin(x + k \cdot 360^\circ)\quad \text{und}\quad \cos(x) = \cos(x + k \cdot 360^\circ)\,.
Hierbei bezeichnet k∈Zk \in \Z eine ganze Zahl. Die folgende Tabelle listet die wichtigsten Funktionswerte der beiden trigonometrischen Funktionen auf. Weitere Funktionswerte können auf einer im Abschnitt Weblinks aufgeführten Seite gefunden werden.
Winkel α\alpha (Grad) 0∘0^\circ 30∘30^\circ 45∘45^\circ 60∘60^\circ 90∘90^\circ 180∘180^\circ 270∘270^\circ 360∘360^\circ
Bogenmaß 00 π6\frac{\pi}{6} π4\frac{\pi}{4} π3\frac{\pi}{3} π2\frac{\pi}{2} π\pi 3π2\frac{3\pi}{2} 2π2\pi
Sinus 00 12\frac12 122\frac12\sqrt2 123\frac12\sqrt3 1 1 0 0 −1-1 00
Kosinus 1 1 123\frac12\sqrt3 122\frac12\sqrt2 12\frac12 0 0 −1-1 0 0 1 1
Zur Herleitung siehe Tabelle 7CGF.

Weitere mit Quadratwurzeln angebbare Funktionswerte

Über die Berechnung der fünften Einheitswurzeln mittels einer quadratischen Gleichung ergibt sich
sin⁡(18∘)=cos⁡(72∘)=5−14\sin(18^\circ)=\cos(72^\circ)=\frac{\sqrt{5}-1}{4}.
Mit Hilfe der Additionstheoreme lassen sich viele weitere solche Ausdrücke berechnen wie beispielsweise die Seitenlänge eines regulären Fünfecks über
cos⁡(54∘)=sin⁡(2⋅18∘)=125−52\cos(54^\circ)=\sin(2\cdot18^\circ)=\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{2}}
und sin⁡(15∘)\sin(15^\circ), woraus folgt
32=cos⁡(30∘)=cos⁡2(15∘)−sin⁡2(15∘)=1−2sin⁡2(15∘)\frac{\sqrt{3}}{2}=\cos(30^\circ)=\cos^2(15^\circ)-\sin^2(15^\circ)=1-2\sin^2(15^\circ).
Aus sin⁡(18∘)\sin(18^\circ) und sin⁡(15∘)\sin(15^\circ) lassen sich dann z. B. sin⁡(3∘)\sin(3^\circ) und dann rekursiv auch alle sin⁡(k⋅3∘)\sin(k \cdot 3^\circ), k∈Z  k\in\Z\; ermitteln.
Generell gilt, dass sin⁡α  \sin\alpha\; und cos⁡α  \cos\alpha\; genau dann explizit mit den vier Grundrechenarten und Quadratwurzeln darstellbar sind, wenn der Winkel α  \alpha\; mit Zirkel und Lineal konstruierbar ist, insbesondere also wenn α  \alpha\; von der Gestalt
α=k360∘2np1…pr\alpha=k\frac{360^\circ}{2^np_1\dots p_r}
ist, wobei k∈Z  k\in\Z\;, n∈N0  n\in\N_0\; und die pi  p_i\; für i=1,…,r  i=1,\dots,r\; Fermatsche Primzahlen sind.In obigem Beispiel von α=3∘\alpha=3^\circ ist k=1  k=1\; und der Nenner gleich 120=23⋅3⋅5.120=2^3\cdot 3\cdot 5.

Umkehrfunktion

Die Umkehrfunktionen
arcsin ⁣:[−1,1]→[−90∘,90∘]arccos ⁣:[−1,1]→[0∘,180∘]\begin{array}{cl} \text{arcsin} \colon [-1,1] &\to [-90^\circ, 90^\circ] \\ \text{arccos}\colon [-1,1] &\to [0^\circ, 180^\circ] \end{array}
werden Arkussinus bzw. Arkuskosinus genannt.

Ableitung und Integration von Sinus und Kosinus

Ableitung

Wird x  x\; im Bogenmaß angegeben, so gilt für die Ableitung der Sinusfunktion
sin⁡′(x)=cos⁡(x)\sin^\prime(x) = \cos(x)
Aus cos⁡(x)=sin⁡(π2−x)\cos(x)=\sin\left(\tfrac{\pi}{2}-x\right) und der Kettenregel erhält man die Ableitung des Kosinus:
cos⁡′(x)=−sin⁡(x)\cos^\prime(x) = -\sin(x).

Stammfunktion

Aus den Ergebnissen über die Ableitung ergibt sich unmittelbar die Stammfunktion von Sinus und Kosinus im Bogenmaß:
∫sin⁡(x) dx=−cos⁡(x)+C\int\sin(x)\,\mathrm{d}x=-\cos(x)+C
∫cos⁡(x) dx=sin⁡(x)+C\int\cos(x)\,\mathrm{d}x=\sin(x)+C

Die Logik ist die Hygiene, deren sich der Mathematiker bedient, um seine Gedanken gesund und kräftig zu erhalten.

Hermann Weyl

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Sinus und Kosinus aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Transzendente Funktionen