Analytische Geometrie der Ebene

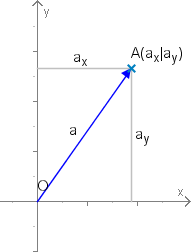
Ebene.png
Einen Punkt AA der euklidischen Ebene R2\dom {R ^2} kann man als Ortsvektor aa auffassen, der durch eine xx- und eine yy-Koordinate charakterisiert ist. Man schreibt dann A(ax; ay)A(a_x;\, a_y) oder A(ax∣ay)A(a_x|a_y).
Der Vektor wird häufig in Spaltenschreibweise als:
a=(axay) a=\pmatrix { a_x\\ a_y}
angegeben.
Der Abstand dd des Punktes AA vom Ursprung entspricht genau der Norm des Vektors aa (Schreibweise: ∣∣a∣∣||a||) und wird mit der üblichen euklidischen Metrik ermittelt, die elementargeometrisch dem Satz des Pythagoras entspricht:
d=∣∣a∣∣=ax2+ay2d=||a||=\sqrt {a_x^2+a_y^2}
Für zwei Punkte A(ax∣ay)A(a_x|a_y) und B(bx∣by)B(b_x|b_y) ergibt sich dem Abstand dd voneinander mit:
d=∣∣a−b∣∣=(ax−bx)2+(ay−by)2d=||a-b||=\sqrt{(a_x-b_x)^2+(a_y-b_y)^2 },
was genau der Norm der Differenz entspricht.
 
 

Eine mathematische Wahrheit ist an sich weder einfach noch kompliziert, sie ist.

Émile Lemoine

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Geometrie