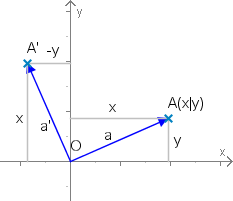
Orthokomplement

Ortho.png
Eine Besonderheit der euklidischen Ebene ist das Orthokomplement a⊥{a}\ortho eines Ortsvektors a=(xy)a=\pmatrix { {x}\\{y}}. Dies bildet in natürlicher Weise wieder einen Ortsvektor und wir definieren es mit
a⊥=(−yx){a}\ortho =\pmatrix { {\uminus y}\\ {x}}
Also geht a⊥{a}\ortho aus aa durch Drehung um 90° hervor.

Satz 5309A (Eigenschaften des Orthokomplements)

Für Ortsvektoren aa,bb der euklidischen Ebene und reelle Zahlen t∈Rt\in\dom R gilt:
  1. (a⊥)⊥=−a({a}\ortho)\ortho=\uminus a
  2. (a+b)⊥=a⊥+b⊥(a+b)\ortho={a}\ortho+{b}\ortho
  3. (ta)⊥=t⋅a⊥(ta)\ortho =t\cdot {a}\ortho
  4. ⟨a⊥,a⟩=0\spo{a}\ortho , a\spc=0
  5. ⟨a⊥,b⟩=−⟨a,b⊥⟩\spo a\ortho, b\spc=-\spo a,b\ortho\spc
  6. ∣∣a⊥∣∣=∣∣a∣∣||{a}\ortho||=||a||
Damit ist  ⊥:R2→R2\, \ortho: \dom{R^2}\rightarrow \dom {R^2} eine lineare Abbildung.
 
 

Beweis

Die Behauptungen hat man durch Einsetzen in die Definition schnell nachgerechnet. □\qed

Satz 5324A (Orthokomplement und Skalarprodukt)

Für drei Vektoren aa, bb und cc der euklidischen Ebene gilt:
  1. ⟨a,b⟩2+⟨a,b⊥⟩2=∣∣a∣∣2∣b∣∣2=⟨a,a⟩⟨b,b⟩\spo a,b\spc^2+\spo a,b\ortho\spc^2=||a||^2|b||^2=\spo a,a\spc\spo b,b\spc
  2. ⟨a,b⊥⟩c+⟨b,c⊥⟩a+⟨c,a⊥⟩b=0\spo a,b\ortho\spc c+ \spo b,c\ortho\spc a +\spo c,a\ortho\spc b=0
Dabei drückt ii. insbesondere aus, dass je drei Vektoren des R2\dom{R^2} linear abhängig sind.
Weiterhin kann man aus i. die Cauchy-Schwarzsche Ungleichung ableiten, die aber schon im Satz 5310C für allgemeine euklidische Vektorräume bewiesen wurde.

Beweis

Wir setzen a=(axay)a=\pmatrix { {a_x}\\{a_y}}, b=(bxby)b=\pmatrix { {b_x}\\{b_y}}.
(i): Mit b⊥=(−bybx)b\ortho=\pmatrix { {-b_y}\\{b_x}} ergibt sich ⟨a,b⟩2+⟨a,b⊥⟩2\spo a,b\spc^2+\spo a,b\ortho\spc^2 =(axbx+ayby)2+(−axby+aybx)2=(a_xb_x+a_yb_y)^2+(-a_xb_y+a_yb_x)^2 =(axbx)2+(ayby)2+2axaybxby=(a_xb_x)^2+(a_yb_y)^2+2a_xa_yb_xb_y+(axby)2+(aybx)2−2axaybxby+(a_xb_y)^2+(a_yb_x)^2-2a_xa_yb_xb_y =(axbx)2+(ayby)2+(axby)2+(aybx)2=(a_xb_x)^2+(a_yb_y)^2+(a_xb_y)^2+(a_yb_x)^2 =(ax2+ay2)(bx2+by2)=({a_x}^2+{a_y}^2)({b_x}^2+{b_y}^2) =∣∣a∣∣2∣b∣∣2=||a||^2|b||^2.
(ii): Mit c=(cxcy)c=\pmatrix { {c_x}\\{c_y}} bedeutet die Behauptung: (−axby+aybx)c+(−bxcy+bycx)a(-a_xb_y+a_yb_x)c+(-b_xc_y+b_yc_x)a+(−cxay+cyax)b=0+(-c_xa_y+c_ya_x)b=0. Wenn wir diese Vektorgleichung für xx und yy komponentenweise aufschreiben, ersieht man die Gültigkeit der beiden entstehenden Gleichungen sofort. □\qed

Es gibt keinen Königsweg zur Mathematik.

Euklid

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analytische Geometrie