Dreiecke

Drei Vektoren aa, bb und cc spannen ein (entartetes) Dreieck auf.

Flächeninhalt

Aus der Elementargeometrie wissen wir (Formel 5504A) , dass der Flächeninhalt sich als Produkt von einer Grundseite und der halben Höhe ergibt.
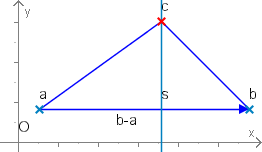
FlDreieck.png
Die Höhe durch cc steht senkrecht auf b−ab-a und hat damit eine Geradengleichung der Form
c+α(b−a)⊥c+\alpha(b-a)\ortho.(1)
Für den Schnittpunkt ss der Höhe mit der gegenüberliegenden Seite gilt:
s=a+β(b−a)=c+α(b−a)⊥s=a+\beta(b-a)=c+\alpha(b-a)\ortho.(2)
Multiplizieren wir diese Gleichung mit (b−a)⊥(b-a)\ortho erhalten wir
⟨a,(b−a)⊥⟩=⟨c,(b−a)⊥⟩+α⟨(b−a)⊥,(b−a)⊥⟩\spo a, (b-a)\ortho\spc=\spo c, (b-a)\ortho\spc+\alpha\spo (b-a)\ortho,(b-a)\ortho\spc,(3)
woraus sich
α∣∣(b−a)⊥∣∣2=⟨a−c,b⊥−a⊥⟩\alpha||(b-a)\ortho||^2= \spo a-c, b\ortho-a\ortho\spc(4)
Die Länge der Höhe ist ∣∣s−c∣∣||s-c|| und mit (2) ergibt sich zu
∣∣s−c∣∣=∣α∣⋅∣∣(b−a)⊥∣∣||s-c||=|\alpha|\cdot ||(b-a)\ortho||,(5)
und mit (4) haben wir wegen ∣∣(b−a)⊥∣∣=∣∣b−a∣∣||(b-a)\ortho||=||b-a||
∣∣s−c∣∣=∣⟨a−c,b⊥−a⊥⟩∣∣∣b−a∣∣||s-c||=\dfrac{|\spo a-c, b\ortho-a\ortho\spc|}{||b-a||}.(6)
Setzen wir jetzt
[a,b,c]:=⟨a⊥,b⟩+⟨b⊥,c⟩+⟨c⊥,a⟩[a,b,c]:=\spo a\ortho, b\spc +\spo b\ortho, c\spc +\spo c\ortho, a\spc,(7)
können wir einfach zeigen, dass
⟨a−c,b⊥−a⊥⟩=−[a,b,c]\spo a-c, b\ortho-a\ortho\spc=-[a,b,c],(8)
und (6) erhält die Form
∣∣s−c∣∣=∣[a,b,c]∣∣∣a−b∣∣||s-c||=\dfrac{|[a,b,c]|}{||a-b||}.(9)
Und schließlich erhalten wir

Formel 5504B (Flächeninhalt des Dreiecks)

A=12∣[a,b,c]∣A=\dfrac 1 2 |[a,b,c]|(10)
Wir erhalten außerdem ein einfaches Kriterium, dafür, dass das Dreieck nicht entartet ist, drei Punkte also nicht auf einer Geraden liegen.
Drei Punkte aa, bb und cc liegen genau dann auf einer Geraden, wenn [a,b,c]=0 gilt.
 
 

Miß alles, was sich messen läßt, und mach alles meßbar, was sich nicht messen läßt.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analytische Geometrie