Flächeninhalt des Dreiecks

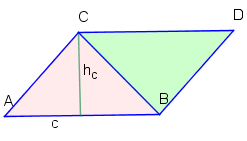
DreieckFlaecheninhalt.png
Um den Flächeninhalt eines Dreiecks zu bestimmen, betrachten wir die nebenstehende Abbildung.
Das Dreieck ΔABC\Delta ABC wird durch Spiegelung an der Seite BC‾\overline{BC} zum Parallelogramm ABDCABDC. Bezeichnen wir seinen Flächeninhalt mit APA_P, so wissen wir aus der Flächenformel fürs Parallelogramm, dass AP=c⋅hcA_P=c\cdot h_c. Für den Flächeninhalt des Dreiecks AA gilt demnach
 
 

Formel 5504A (Flächeninhalt des Dreiecks)

A=c⋅hc2A=\dfrac{c\cdot h_c}{2}(1)
Analoge Formeln gelten für die anderen Seiten und ihre Höhen, so dass man allgemein sagen kann:
Der Flächeninhalt eines Dreiecks ist das Produkt aus der Länge einer Seite und der halben Länge der dazugehörigen Höhe.
Benutzen wir die Beziehung sin⁡α=hcb\sin\alpha=\dfrac{h_c} b, also hb=b⋅sin⁡αh_b=b\cdot\sin\alpha und setzen diese in (1) ein, so erhalten wir den Flächeninhalt ausgedrückt durch zwei Seiten und den eingeschlossenen Winkel

Formel 5518B (Dreiecksfläche aus zwei Seiten und dem eingeschlossenen Winkel)

A=12bc⋅sin⁡α=12ab⋅sin⁡γ=12ac⋅sin⁡βA=\dfrac 1 2 bc\cdot\sin \alpha =\dfrac 1 2 ab\cdot\sin \gamma =\dfrac 1 2 ac\cdot\sin \beta
Dabei können die Seiten und Winkel wieder zyklisch vertauscht werden.
Da die Höhe im Dreieck nicht immer zur Verfügung steht, stellt sich die Frage, wie man den Flächeninhalt alleinig aus den Längen der drei Seiten berechnet. Dafür gibt es die Flächenformel nach Heron:

Formel 5518A (Heronsche Flächenformel)

A=s(s−a)(s−b)(s−c)=ρ⋅s=uρ2A=\sqrt{s(s-a)(s-b)(s-c)}=\rho\cdot s=\dfrac{u\rho}2
In dieser Formel sind aa, bb und cc die Dreiecksseiten und s=a+b+c2s=\dfrac{a+b+c}2 der halbe Umfang und ρ\rho der Radius des Inkreises.
Die Heronische Flächenformel kann als Spezialfall der Formel von Brahmagupta, die den Inhalt eines Sehnenvierecks berechnet, aufgefasst werden. Sie ergibt sich aus dieser wenn die Länge einer Vierecksseite 0 ist. Die folgende Herleitung greift jedoch nicht darauf zurück, sondern verdeutlicht den Zusammenhang von Inkreisradius und Flächeninhalt.

Herleitung

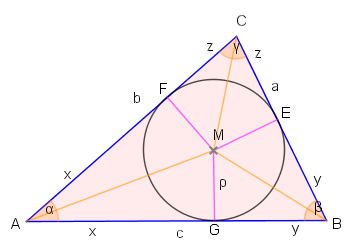
DreieckInnenkreis.png
Sehen wir uns die Abbildung an, die wir zur Herleitung der Formel für den Inkreisradius des Dreiecks benutzt haben.
Es ist unmittelbar ersichtlich, dass der Flächeninhalt AA des Dreiecks die Summe der paarweise kongruenten Teildreiecke ist. Damit gilt: A=ρ(x+y+z)A=\rho(x+y+z).
Wir wissen außerdem (Satz 5515J), dass ρ=(s−a)(s−b)(s−c)s\rho=\sqrt {\dfrac {(s-a)(s-b)(s-c)}{s}} und s=x+y+zs=x+y+z (siehe die entsprechenden Überlegungen zum Inkreis).
Damit erhalten wir: A=s⋅(s−a)(s−b)(s−c)sA= s\cdot \sqrt{ \dfrac {(s-a)(s-b)(s-c)}{s}} == s(s−a)(s−b)(s−c)\sqrt{s(s-a)(s-b)(s-c)}

Formel B449 (Flächeninhalt aus einer Seite und zwei anliegenden Winkeln)

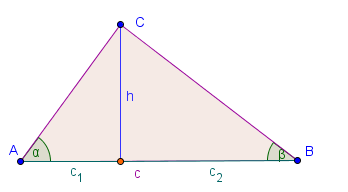
flcot.png
A=c22(cot⁡α+cot⁡β)A=\dfrac {c^2}{2(\cot\alpha+\cot\beta)}
Da wegen des Innenwinkelsatzes zwei Winkel im Dreieck den dritten immer eindeutig bestimmen, kann mittels dieser Formel der Flächeninhalt eines jeden Dreiecks bei dem zwei beliebige Winkel und eine Seite gegeben sind, bestimmt werden.

Herleitung

Nach Definition des Kotangens gilt cot⁡α=c1h\cot\alpha=\dfrac{c_1}h und cot⁡β=c2h\cot\beta=\dfrac{c_2}h. Nach Formel 5504A gilt A=12c⋅h=12c2⋅hc1+c2A=\dfrac 1 2 c\cdot h=\dfrac 1 2 \dfrac {c^2\cdot h}{c_1+c_2} =12c2⋅hh(cot⁡α+cot⁡β)=\dfrac 1 2 \dfrac {c^2\cdot h}{h(\cot\alpha+\cot\beta)} =c22(cot⁡α+cot⁡β)=\dfrac {c^2}{2(\cot\alpha+\cot\beta)}.

Ein guter mathematischer Scherz ist immer besser als ein ganzes Dutzend mittelmäßiger gelehrter Abhandlungen.

John Edensor Littlewood

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie