Winkelhalbierende und Inkreis im Dreieck

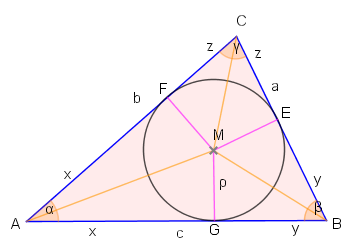
DreieckInnenkreis.png
Unter den Winkelhalbierenden versteht man diejenigen Geraden, welche die Innenwinkel des Dreiecks halbieren.
Es gilt der folgende Satz.

Satz 5515H (Winkelhalbierende und Inkreis)

Die Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt, dem Mittelpunkt des Inkreises.

Beweis

Jeder Punkt der Winkelhalbierenden von α\alpha hat den gleichen Abstand zu Seite bb und Seite cc. Ein analoger Schluss gilt für die Winkelhalbierende von β\beta. Alle Punkte auf dieser haben von den Seiten aa und cc den gleichen Abstand. Damit hat der Schnittpunkt MM der beiden Winkelhalbierenden den gleichen Abstand ρ\rho von den Seiten aa, bb und cc. Also ist dieser Punkt Mittelpunkt des Inkreises.
Für die Winkelhalbierende von γ\gamma können wir damit auch schließen, dass sie durch den Punkt MM geht.□\qed
 
 

Satz 5515J (Inkreisradius)

In einem beliebigen Dreieck kann man den Radius des Innenkreises mit der Formel
ρ=(s−a)(s−b)(s−c)s\rho=\sqrt{ \dfrac {(s-a)(s-b)(s-c)}{s}}(1)
bestimmen. Dabei ist ss der halbe Umfang:
s=a+b+c2s=\dfrac{a+b+c}2.(2)

Beweis

In der Abbildung ist MM ist der Schnittpunkt der Winkelhalbierenden; EE, FF und GG sind die Lotfußpunkte von MM aus auf die Dreiecksseiten aa, bb und cc.
Man findet die x,y,zx,y,z als Teilstrecken der Dreicksseiten a,b,ca,b,c wieder. Man überzeugt sich leicht, dass die mit xx bezeichnete Seite AG‾\overline{AG} gleichlang wie die mit xx bezeichnete Strecke AF‾\overline{AF} ist, da ΔAGM\Delta AGM kongruent zu ΔAMF\Delta AMF ist. Sie stimmen in der Seite AM‾\overline {AM} sowie zwei Winkeln (einem rechten und α2\dfrac \alpha 2 überein). Analoges gilt für die mit yy und zz bezeichneten Strecken.
Aus der Abbildung ersieht man außerdem, dass:
c=x+yc=x+y, b=x+zb=x+z und a=y+za=y+z.(3)
gilt. Aus (2) und (3) erhalten wir s=x+y+zs=x+y+z und damit
x=s−ax=s-a, y=s−by=s-b und z=s−cz=s-c.(4)
Um den Inkreisradius ρ\rho zu erhalten, gehen wir von der Definition des Tangens aus und lesen aus der obigen Graphik die Beziehung
tan⁡α2=ρx=ρs−a\tan\dfrac{\alpha}{2}=\dfrac{\rho}{x}=\dfrac{\rho}{s-a}(5)
ab. Damit gilt also:
ρ=(s−a)tan⁡α2\rho=(s-a) \tan\dfrac{\alpha}{2}.(6)
Analog kann man entsprechende Formeln für die anderen Seiten und Winkel herleiten.
Setzen wir tan⁡α2=(s−b)(s−c)s(s−a)\tan{ \dfrac \alpha 2} = \sqrt{ \dfrac {(s-b)(s-c)}{s(s-a)}} (Halbwinkelsatz) in (6) ein, ergibt sich:
ρ=(s−a)(s−b)(s−c)s(s−a)\rho=(s-a) \sqrt {\dfrac {(s-b)(s-c)}{s(s-a)}} =(s−a)2(s−b)(s−c)s(s−a)=\sqrt{ \dfrac {(s-a)^2(s-b)(s-c)}{s(s-a)}},(7)
woraus sich die Behauptung (1) nach Kürzen von (s−a)(s-a) ergibt. □\qed

So seltsam es auch klingen mag, die Stärke der Mathematik beruht auf dem Vermeiden jeder unnötigen Annahme und auf ihrer großartigen Einsparung an Denkarbeit.

Ernst Mach

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Das Dreieck