Höhen im Dreieck

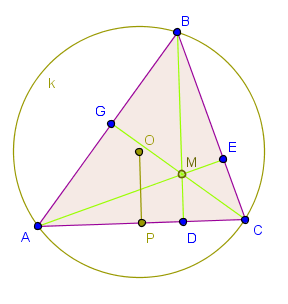
Die Höhen erhält man, indem man von den Ecken aus die Lote auf die gegenüberliegenden Seiten fällt. In der Abbildung sind dies die Strecken $\ovl{AE }$, $\ovl{BD }$ und $\ovl{CG }$

Die Höhen eines Dreiecks schneiden sich in einem Punkt ($M$ in der Abbildung). Außerdem gilt: die Abstände der Eckpunkte vom Höhenschnittpunkt sind doppelt so groß wie die Abstände des Umkreismittelpunkts $O$ von der jeweils gegenüberliegenden Seite. Beispielsweise ist die Strecke $\ovl{BM}$ doppelt so lang wie $\ovl{OP}$

Den Beweis führen wir, indem wir den Höhenschnittpunkt als Schnittpunkt der Mittelsenkrechten eines Dreiecks zurückführen.

Im $\Delta ABC$ zeichnen wir die Parallelen zu den einzelnen Seiten durch die gegenüberliegenden Punkte. So entsteht das Dreieck $\Delta HIJ$. Wir zeigen jetzt, dass $A$ die Seite $\overline{JH}$ halbiert und entsprechend $B$ die Seite $\overline{HI}$ und $C$ die Seite $\overline{IJ}$

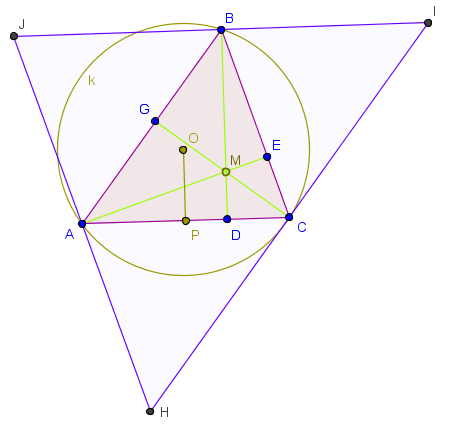
Die Dreiecke $\Delta ACJ$, $\Delta BIC$ und $\Delta AHB$ sind zum Originaldreieck $\Delta ABC$ kongruent. Dies ist folgendermaßen einzusehen: Die Winkel kann man über Stufen- und Wechselwinkelbeziehungen in den Dreiecken wieder finden. Außerdem stimmen sie in jeweils einer Seite überein. Damit kann man zeigen, dass die Strecken $\overline{BC}$, $\overline{AJ}$ und $\overline{AH}$ gleichlang sind. Mit anderen Worten $A$ ist Mittelpunkt der Strecke $\overline{JH}$. Entsprechendes gilt für die anderen Seiten.

Diese Mittelsenkrechten schneiden sich in einem Punkt $M$ (Satz 5515E).

Auf Grund der Konstruktion sind sie aber gerade auch die Höhen im Dreieck $\Delta ABC$, womit wir gezeigt hätten, dass sich diese auch in einem Punkt schneiden müssen.

Ist $O$ der Umkreismittelpunkt von $\Delta ABC$ und $P$ der Lotfußpunkt auf die Seite $\ovl{AB}$. Wegen der Ähnlichkeit der Dreiecke $\Delta ABC$ und $\Delta HIJ$ entsprechen sich die Strecken $\ovl{OP}$ und $\ovl{MB}$ und da $|\ovl{IJ}|=2|\ovl{AC}|$, gilt auch $|\ovl{MB}|=2|\ovl{OP}|$. $\qed$

Seien $h_a$, $h_b$ und $h_c$ die Höhen in einem Dreieck und $\rho$ der Inkreisradius. Dann gilt:

Für den Flächeninhalt $A$ des Dreiecks gilt nach Formel 5518A wobei der halbe Umfang ist. Umgestellt erhalten wir

Nach Formel 5504A ist andererseits woraus wir erhalten

Vergleichen wir dieses Ergebnis mit (1), so ergibt sich sofort die Behauptung. $\qed$