Das Dreieck
Für eine ausführlich Behandlung des Dreiecks siehe Dreiecksgeometrie.
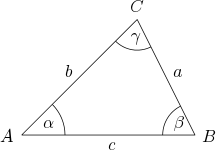
Dreieck mit typische Bezeichnungen
Ein Dreieck ist eine geometrische Figur, die durch drei Punkte definiert wird. Dabei wird vorausgesetzt, dass diese drei Punkte nicht kollinear sind, d.h. sie nicht auf einer Geraden liegen. Sie werden die Eckpunkte oder einfach die Ecken des Dreiecks genannt. Die Verbindungsstrecken zwischen je zwei Ecken - die auch die Begrenzungslinien des Dreiecks bilden - heißen Seiten des Dreiecks. Die Innenwinkel sind die von je zwei an einem Eckpunkt zusammentreffenden Seiten gebildete Winkel.
Bezeichnungen
Die [!Abbildung] zeigt ein allgemeines Dreieck mit typischen Bezeichnungen. Die Eckpunkte des Dreiecks werden mit Großbuchstaben wie , und bezeichnet üblicherweise wie in der [!Abbildung] im mathematisch positiven Drehsinn, also entgegen dem Uhrzeiger. Die den Ecken gegenüberliegenden Seiten werden mit den entsprechen Kleinbuchstaben wie , und bezeichnet. Es ist aber auch eine Bezeichnung wie bei allgemeinen Strecken üblich. Hier stünde dann für die Seite . Für die Innenwinkel werden wie bei Winkeln üblich kleine griechische Buchstaben verwendet, wie z.B. , und .
Da keine der Seiten bzw. keiner der Winkel eines Dreiecks ausgezeichnet ist, kann man alle Beziehungen und Formeln die diese Größen enthalten durch zyklisches Vertauschen ineinander überführen. Wir geben meistens alle Formeln an, beweisen diese jedoch häufig nur für eine [!Kombination] von Seiten und Winkel.
Inhalt
- Dreiecksarten
- Innenwinkel
- Dreiecksungleichung
- Flächeninhalt
- Kongruenz
- Besondere Linien
- Spezielle Dreiecke
- Trigonometrische Sätze
- Weitere Sätze
- Dreiecksberechnung
- Aufgaben
Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.
Richard Feynman
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе