Das Viereck
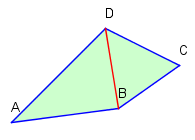
Abb. 1: Konvexes Viereck
Vier voneinander verschiedene Punkte, von denen keine drei auf einer Geraden liegen, legen ein Viereck fest. Wir gehen hier vom konvexen Viereck aus. Anschaulich heißt das, dass es keinen "Knick nach innen" hat. Mathematisch formuliert: Mit je zwei Punkten innerhalb des Vierecks liegt auch ihre Verbindungsstrecke innerhalb.
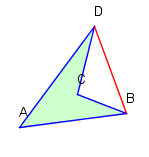
Abb. 2: Konkaves Viereck
Abb. 1 zeigt ein konvexes Viereck und Abb.2 ein konkaves.
Verbindet man zwei nicht durch eine Seite verbundene Punkte, erhält man eine Diagonale (z.B. in Abb. 1).
Satz IL71 (Innenwinkelsumme im Viereck)
Die Summe der Innenwinkel im Viereck beträgt 360°.
Dies ist leicht einzusehen: Zeichnet man eine Diagonale ein, so erhält man zwei Dreiecke. Die Summe der Innenwinkelsummen dieser Dreiecke ergibt aber gerade die Innenwinkelsumme des Vierecks.
Daraus folgt, dass es keine "spitzwinkligen" Vierecke (Vierecke nur mit spitzen Winkeln) geben kann. Denn gäbe es diese, wäre ihre Innenwinkelsumme kleiner als 360°. Damit muss jedes Viereck (wenn es kein Rechteck ist) wenigstens einen rechten oder stumpfen Innenwinkel enthalten.
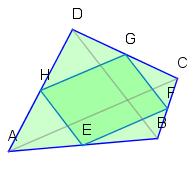
Satz 5512A
Wenn man die Mittelpunkte der Seiten eines Vierecks verbindet, erhält man ein Parallelogramm.
Beweis
Auf Grund des Strahlensatzes kann man zeigen, dass und , womit dann auch . Analog kann man nachweisen, dass die beiden anderen Seiten parallel sind.
Das ist ein Mittel, das Paradies nicht zu verfehlen: auf der einen Seite einen Mathematiker, auf der anderen einen Jesuiten; mit dieser Begleitung muß man seinen Weg machen, oder man macht ihn niemals.
Friedrich der Große
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе