Das Rechteck

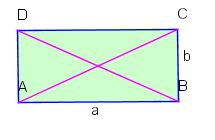
Rechteck.png
Ein Viereck mit vier rechten Innenwinkeln heißt Rechteck. (Es genügt drei rechte Innenwinkel zu fordern, da der vierte dann wegen der Innenwinkelsumme ebenfalls ein rechter Winkel sein muss)

Satz 16GH (Charakterisierung des Rechtecks)

Jedes Rechteck ist ein Parallelogramm.
Ein Parallelogramm ist genau dann ein Rechteck wenn wenigstens eine der folgenden Bedingungen gilt

Beweis

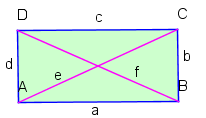
RechteckV.png
Um nachzuweisen, dass jedes Rechteck ein Parallelogramm ist, zeigt man, dass gegenüberliegende Seiten gleich lang sind (Satz 16GF).
Nach Satz des Pythagoras ergibt sich: a2+b2=e2=c2+d2a^2+b^2=e^2=c^2+d^2 und b2+c2=f2=a2+d2b^2+c^2=f^2=a^2+d^2, woraus man die beiden Gleichungen a2−c2=c2−a2a^2-c^2=c^2-a^2 und b2−d2=d2−b2b^2-d^2=d^2-b^2 ableiten kann, womit a=ca=c und b=db=d gilt.
Für den Beweis des zweiten Teils sei nun ein Parallelogramm gegeben. Ist ein Innenwinkel rechtwinklig, so müssen trivialerweise auch alle anderen Winkel rechte sein.
In einem Rechteck sind die Diagonalen gleich lang, da es sich nach dem oben Bewiesenen um ein Parallelogramm mit rechten Winkeln handelt. In diesem können wir den Satz des Pythagoras anwenden und erhalten für beide Diagonalen e2=a2+b2=f2e^2=a^2+b^2=f^2, also e=fe=f.
Sind andererseits in einem Parallelogramm die Diagonalen gleich lang, so gilt nach der Parallelogrammgleichung e2=f2=a2+b2e^2=f^2=a^2+b^2 und mit der Umkehrung des Satzes des Pythagoras erhalten wir, dass die Innenwinkel rechte Winkel sind, es sich mithin um ein Rechteck handelt. □\qed

Die Länge der Diagonalen dd ergibt sich aus dem Satz des Pythagoras mit d=a2+b2d=\sqrt{a^2+b^2}. Beide Diagonalen sind offensichtlich gleich lang.

Flächeninhalt

A=a⋅bA=a\cdot b

Umfang

u=2⋅(a+b)u=2\cdot(a+b)
 
 

Die Logik ist die Hygiene, deren sich der Mathematiker bedient, um seine Gedanken gesund und kräftig zu erhalten.

Hermann Weyl

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie