Das Sehnenviereck

Liegen alle vier Eckpunkte eines Vierecks auf einem Kreis, dann spricht man von einem Sehnenviereck; damit sind die Seiten des Vierecks Sehnen des Kreises. Mit anderen Worten ist ein Sehnenviereck, ein Viereck, dem sich ein Kreis umschreiben lässt.

Ein Viereck ist genau dann ein Sehnenviereck, wenn sich gegenüberliegende Winkel zu 180° ergänzen. Da die Innenwinkelsumme im Viereck 360° beträgt, reicht es, wenn sich 2 gegenüberliegende Winkel zu 180° ergänzen, da dies dann für das andere Winkelpaar automatisch folgt.

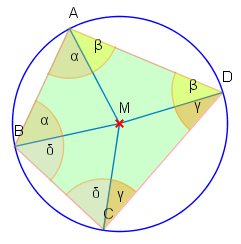
$\implies$ Sei das Sehnenviereck $ABCD$ in nebenstehender Grafik dadurch in Teildreiecke zerlegt, dass die einzelnen Ecken mit dem Mittelpunkt des Kreises $M$ verbunden werden.

Das Dreieck $\triangle ABM$ ist gleichschenklig, damit sind die Winkel $\angle ABM$ und $\angle MAB$ gleich groß. Dieser Winkel ist mit $\alpha$ bezeichnet. Analoge Schlüsse gelten für die anderen Teildreiecke und Winkel in nebenstehender Grafik. Für die Innenwinkelsumme des Vierecks ergibt sich dann

also auch

woraus sich sofort die Behauptung ergibt.

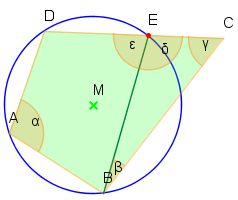
$\Leftarrow$: Gelte nun im Viereck $ABCD$ $\alpha+\gamma=180°$. Wir bilden den Umkreis zum Dreieck $ABD$ und zeigen, dass $C$ auf diesem Kreis liegt. Angenommen $C$ liegt nicht auf dem Kreis. Dann gibt es einen Punkt $E$ auf der Geraden durch $D$ und $C$, der auf dem Kreis liegt. Für das Sehnenviereck $ABED$ gilt nach dem oben Bewiesen $\alpha+\epsilon=180°$ und mit der Voraussetzung gilt $\gamma=\epsilon$. Im Dreieck $BCE$ gilt nach dem Innenwinkelsatz für Dreiecke $\beta+\gamma+\delta=180°$ und außerdem ist $\delta+\epsilon=180°$. Also $\beta+\gamma=\epsilon$. Da $\beta>0$ ist dies ein Widerspruch zu $\gamma=\epsilon$. Damit muss $C$ auf dem Kreis liegen. $\qed$

Damit kann kein Innenwinkel eines Sehnenvierecks größer als 180° sein und wir erhalten:

Jedes Sehnenviereck ist konvex.