Konvexe Mengen

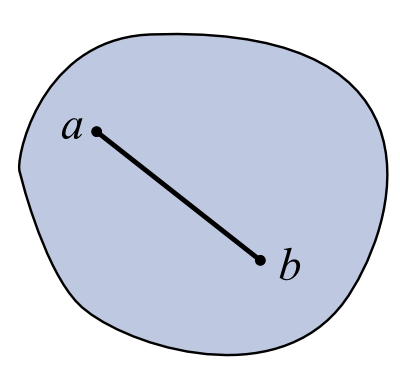
ConvexMenge.png
konvexe Menge
Anschaulich bedeutet konvex: ohne Löcher oder Einbuchtungen. Mathematisch lässt sich diese Forderung folgendendermaßen ausdrücken: Eine Menge MM heißt konvex, wenn mit je zwei beliebigen Elementen aa und bb aus MM auch ihre Verbindungsstrecke zu MM gehört.
Die beiden [!Abbildungen] rechts veranschaulichen den Unterschied zwischen konvex und nichtkonvexe sehr deutlich. In der oberen Figur können wir zwei beliebige Punkte wählen, diese durch eine Strecke verbinden und wir sehen, dass alle Punkte dieser Strecke stets auch zur Figur gehören. In der unteren Figur reicht schon die eingezeichnete Strecke, um sofort zu erkennen, das sie nicht konvex ist.
 
 
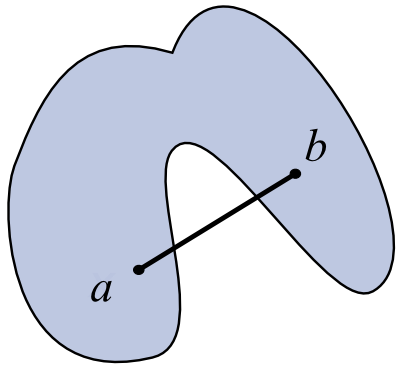
NConvexMenge.png
nichtkonvexe Menge

Definition

Um die Konvexität von Mengen exakt definieren zu können, muss es möglich sein, den Begriff "Strecke" zu definieren.
Sei VV ein reeller (oder komplexer) Vektorraum. Für a,b∈Va, b\in V heißt die Menge
ab‾:={λa+(1−λ)b∣0≤λ≤1}⊆V\overline{ab} := \{\lambda a+(1-\lambda)b\mid0\leq\lambda\leq1\} \subseteq V.
die Verbindungsstrecke zwischen aa und bb.
Eine Teilmenge M⊆VM\subseteq V heißt konvex, genau dann wenn für zwei beliebige Elemente aa, bb aus MM auch ihre Verbindungsstrecke zu MM gehört, also
a,b∈M   ⟹   ab‾⊆Ma, b\in M\,\implies\, \ovl{ab}\subseteq M.

Beispiele

Triviale Beispiele

Die leere Menge ∅\OO, alle einelementigen Mengen, sowie der Vektorraum VV selbst sind konvex. Beliebige Verbindungsstrecken oder -geraden zwischen zwei Punkten aus VV sind konvex.

Ebene Figuren

Dreiecke, Quadrate und alle regulären Polygone sind konvex, ebenso die Kreise. Im allgemeinen müssen Viereck nicht konvex sein. Trapez, Parallelogramme, Sehnenvierecke, Rhomben und Rechtecke sind konvex. Bei den Drachenvierecken gibt es konvexe wie auch nichtkonvexe Vertreter.
Besitzt ein Figur ein Loch, wie z.B. der Kreisring, so ist sie stets nichtkonvex.

Räumliche Figuren

Würfel, Tetraeder und die anderen regulären Polyeder sind konvex, ebenso wie Kugeln und Ellipsoide. Der Torus ist nichtkonvex.
Ebenen und Halbebenen sind konvex.

Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Lineare Algebra