Der Rhombus

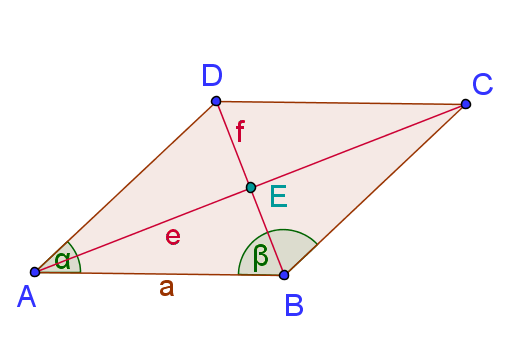
RhombNeu.png
Ein konvexes Viereck, dessen vier Seiten gleichlang sind heißt Rhombus oder Raute . Rhomben sind spezielle Parallelogramme und Drachenvierecke. Ist in einem Rhombus außerdem wenigstens ein Innenwinkel ein rechter (also dann auch alle), so handelt es sich um ein Quadrat.

Satz (Eigenschaften des Rhombus)

Für einen beliebigen Rhombus gilt:
  1. Gegenüberliegende Seiten sind parallel, dh. jeder Rhombus ist ein Parallelogramm.
  2. Gegenüberliegende Winkel sind gleich groß.
  3. Die Diagonalen stehen senkrecht aufeinander und halbieren einander. Damit gilt (e2)2+(f2)2=a2\braceNT{\dfrac e 2}^2+\braceNT{\dfrac f 2}^2=a^2
  4. Benachbarte Winkel ergeben zusammen 180°.
  5. Jeder Innenwinkel wird durch eine Diagonale halbiert.
  6. Er besitzt einen Inkreis.
  7. Beide Diagonalen sind Symmetrieachsen.

Beweis

ii) und vii) folgen daraus, dass die Diagonalen den Rhombus in jeweils 2 kongruente Dreiecke zerlegen.
i) folgt aus ii) und der Umkehrung des Stufenwinkelsatzes
iii) Wegen Satz 16GF halbieren sich die Diagonalen und da nach i) ist jeder Rhombus ein Parallelogramm ist.
iv) folgt aus i) und den Stufenwinkelsatz und Nebenwinkelsatz.
v) Durch die beiden Diagonalen wird ein Rhombus in vier kongruente Teildreiecke zerlegt. Wobei zwei ihrer Innenwinkel genau die halbierten α\alpha und β\beta-Winkel sind.
vi) Fällen wir vom Punkt EE Lote auf die vier Seiten, so sind diese, da die vier Teildreiecke kongruent sind, auch gleich lang. Damit ist ein Kreis um EE mit der Länge dieser Lote als Radius ein Inkreis. □\qed

Formeln

Diagonalenlänge

Da die Diagonalen senkrecht aufeinander stehen, kann man mit der Definition der Winkelfunktionen Sinus und Kosinus die folgenden Beziehungen ableiten:
e = 2⋅a⋅cos⁡α2e \, = \, 2 \cdot a \cdot \cos\dfrac{\alpha}{2} =2⋅a⋅sin⁡β2= 2 \cdot a \cdot \sin\dfrac{\beta}{2}
f = 2⋅a⋅sin⁡α2f \, = \, 2 \cdot a \cdot \sin\dfrac{\alpha}{2} =2⋅a⋅cos⁡β2= 2 \cdot a \cdot \cos\dfrac{\beta}{2}

Flächeninhalt

Die folgende Formel ergibt sich aus Satz 5518E und der Tatsache, dass die Diagonalen im Rhombus senkrecht aufeinander stehen:
A=12⋅e⋅fA = \dfrac{1}{2} \cdot e \cdot f =12⋅AC‾⋅BD‾= \dfrac{1}{2} \cdot \overline{AC} \cdot \overline{BD}.
Diese Flächenformel ergibt sich aus der ersten, den Formeln für die Diagonalenlänge und Anwenden der Additionstheoreme für den Sinus:
A = a2⋅sin⁡α=a2⋅sin⁡βA \, = \, a^2 \cdot \sin\alpha = a^2 \cdot \sin\beta.

Umfang

u = 4⋅au \, = \, 4 \cdot a
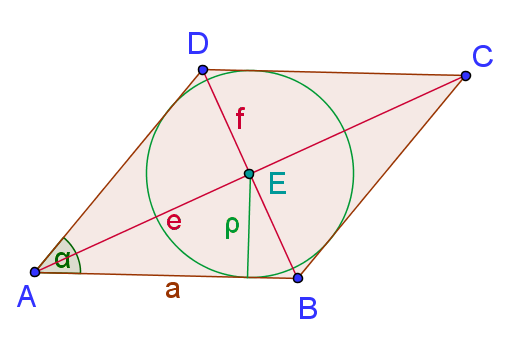
RhombLot.png

Inkreisradius

Es gilt sin⁡α2=ρe2\sin\dfrac \alpha 2=\dfrac \rho {\dfrac e 2}, also ρ=e2sin⁡α2\rho=\dfrac e 2\sin\dfrac \alpha 2 und mit der Länge der Diagonalen: ρ=a⋅cos⁡α2sin⁡α2\rho=a\cdot \cos\dfrac \alpha 2 \sin\dfrac \alpha 2 und mit dem entsprechen Additionstheoreme:
ρ = 12⋅a⋅sin⁡α=12⋅a⋅sin⁡β\rho \, = \, \dfrac{1}{2} \cdot a \cdot \sin\alpha=\dfrac{1}{2} \cdot a \cdot \sin\beta.
 
 

Es gibt Dinge, die den meisten Menschen unglaublich erscheinen, die nicht Mathematik studiert haben.

Archimedes

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie