Additionstheoreme für Sinus und Kosinus

Die Additionstheoreme führen die Berechnung der Winkelfunktionen für die Summe bzw. Differenz von Argumenten auf die Berechnung der Winkelfunktionen für die ursprünglichen Werte zurück. Wenn man den Sinus und Kosinus von zwei Winkeln x1x_1 und x2x_2 kennt, kann man damit auch die Werte für sin⁡(x1+x2)\sin(x_1+x_2) und cos⁡(x1+x2)\cos(x_1+x_2) ermitteln.

Satz 5220A (Additionstheoreme für Sinus und Kosinus)

  1. sin⁡(x1+x2)=sin⁡x1 cos⁡x2+sin⁡x2 cos⁡x1\sin(x_1+x_2) =\sin x_1\, \cos x_2+\sin x_2\, \cos x_1
    sin⁡(x1−x2)=sin⁡x1 cos⁡x2−sin⁡x2 cos⁡x1\sin(x_1-x_2) =\sin x_1\, \cos x_2-\sin x_2\, \cos x_1
    sin⁡2x=2sin⁡x cos⁡x\sin 2x=2\sin x\, \cos x
  2. cos⁡(x1+x2)=cos⁡x1cos⁡x2−sin⁡x1sin⁡x2\cos(x_1+x_2)=\cos x_1\cos x_2- \sin x_1\sin x_2
    cos⁡(x1−x2)=cos⁡x1cos⁡x2+sin⁡x1sin⁡x2\cos(x_1-x_2)=\cos x_1\cos x_2+ \sin x_1\sin x_2
    cos⁡2x=cos⁡2x−sin⁡2x\cos 2x= \cos^2 x- \sin^2 x
Speziell gilt:
  1. sin⁡(π+x)=−sin⁡x\sin(\pi+x)=-\sin x und sin⁡(π−x)=sin⁡x\sin(\pi-x)=\sin x
  2. cos⁡(π+x)=−cos⁡x\cos(\pi+x)=-\cos x und cos⁡(π−x)=−cos⁡x\cos(\pi-x)=-\cos x

Beweis

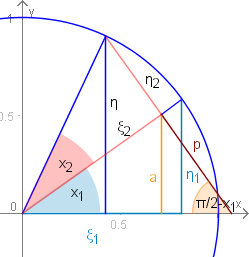
addtheorem.png
i. In der nebenstehenden Grafik sind die beiden Winkel x1x_1 und x2x_2 übereinander abgetragen. Der Kreis soll den Radius 11 haben (Einheitskreis).
Die gesuchte Größe ist η=sin⁡(x1+x2)\eta=\sin(x_1+x_2).
Dann entnimmt man folgende Beziehungen: sin⁡x1=η1\sin x_1 = \eta_1, cos⁡x1=ξ1\cos x_1 = \xi_1, sin⁡x2=η2\sin x_2 = \eta_2, cos⁡x2=ξ2\cos x_2 = \xi_2.
Aus dem Strahlensatz erhält man aξ2=η11\dfrac a {\xi_2}=\dfrac {\eta_1} 1, also a=η1ξ2a=\eta_1\xi_2 und als weitere Beziehung pa=η2+pη\dfrac p a = \dfrac {\eta_2+p} \eta, also η=a(η2+p)p\eta=\dfrac{a(\eta_2+p)} p.
Um pp zu bestimmen, nutzen wir die Beziehung sin⁡(π2−x1)=cos⁡x1\sin\braceNT{\dfrac \pi 2 - x_1}=\cos x_1 =ξ1=ap=\xi_1=\dfrac a p (Satz 5220B).
Damit ergibt sich η=ξ1(η2+p)\eta=\xi_1(\eta_2+p) =ξ1(η2+aξ1)=\xi_1\braceNT{\eta_2+\dfrac a {\xi_1}} =ξ1(η2+η1ξ2ξ1)=\xi_1\braceNT{\eta_2+\dfrac {\eta_1\xi_2} {\xi_1}} =ξ1η2+η1ξ2=\xi_1\eta_2 + \eta_1\xi_2, und wenn wir die Definitionen für Sinus und Kosinus einsetzen erhalten wir die erste Behauptung.
Die beiden anderen Behauptungen ergeben sich trivial wenn wir y=−yy=-y und y=xy=x in die erste Gleichung einsetzen.
ii. Mit Satz 5220B und den Ergebnissen von i. ergibt sich: cos⁡(x1+x2)=sin⁡(π2+x1+x2)\cos(x_1+x_2) = \sin (\dfrac \pi 2 + x_1+x_2) =sin⁡(π2+x1)cos⁡x2+cos⁡(π2+x1)sin⁡x2=\sin(\dfrac \pi 2 + x_1)\cos x_2+\cos(\dfrac \pi 2 + x_1)\sin x_2 =cos⁡x1cos⁡x2−sin⁡x1sin⁡x2=\cos x_1\cos x_2- \sin x_1\sin x_2. Die anderen beiden Behauptungen ergeben sich analog. Die speziellen Aussagen beweist man durch Einsetzen und mit den Werten aus Tabelle 7CGF. □\qed

Satz 5316D (Weitere Additionstheoreme für Sinus und Kosinus)

  1. sin⁡2x=12(1−cos⁡2x)\sin^2x =\dfrac 1 2 (1-\cos 2x)
    cos⁡2x=12(1+cos⁡2x)\cos^2x =\dfrac 1 2 (1+\cos 2x)
  2. sin⁡x1+sin⁡x2=2⋅sin⁡x1+x22⋅cos⁡x1−x22\sin x_1+\sin x_2=2\cdot \sin\dfrac {x_1+x_2} 2\cdot \cos\dfrac {x_1-x_2} 2
    sin⁡x1−sin⁡x2=2⋅cos⁡x1+x22⋅sin⁡x1−x22\sin x_1-\sin x_2=2\cdot \cos\dfrac {x_1+x_2} 2\cdot \sin\dfrac {x_1-x_2} 2
  3. cos⁡x1+cos⁡x2=2⋅cos⁡x1+x22⋅cos⁡x1−x22\cos x_1+\cos x_2=2\cdot \cos\dfrac {x_1+x_2} 2\cdot \cos\dfrac {x_1-x_2} 2
    cos⁡x1−cos⁡x2=−2⋅sin⁡x1+x22⋅sin⁡x1−x22\cos x_1-\cos x_2=-2\cdot \sin\dfrac {x_1+x_2} 2\cdot \sin\dfrac {x_1-x_2} 2

Beweis

(i) sin⁡2x+cos⁡2x=1\sin^2 x+\cos^2 x=1 (Satz 5220B)
  ⟹  2cos⁡2x=1+cos⁡2x−sin⁡2x\implies 2\cos^2 x=1+ \cos^2 x-\sin^2 x
  ⟹  2cos⁡2x=1+cos⁡2x\implies 2\cos^2 x=1+ \cos 2x (Satz 5220A)
  ⟹  12(1+cos⁡2x)\implies \dfrac 1 2 (1+\cos 2x)
Analog zeigt man die Beziehung für den Sinus.
(ii) und (iii). Unter Benutzung von Satz 5220A und Satz 5220B rechnen wir eine Identität exemplarisch vor.
2⋅sin⁡x1+x22⋅cos⁡x1−x222\cdot \sin\dfrac {x_1+x_2} 2\cdot \cos\dfrac {x_1-x_2} 2 =2(sin⁡x12cos⁡x22+cos⁡x12sin⁡x22)(cos⁡x12cos⁡x22+sin⁡x12sin⁡x22)=2\braceNT{\sin\dfrac{x_1} 2\cos\dfrac{x_2} 2 + \cos\dfrac{x_1} 2\sin\dfrac{x_2} 2}\braceNT{\cos\dfrac{x_1} 2\cos\dfrac{x_2} 2 + \sin\dfrac{x_1} 2\sin\dfrac{x_2} 2} =2sin⁡x12cos⁡x12cos⁡2x22+2sin⁡x22cos⁡x22cos⁡2x12=2\sin\dfrac{x_1} 2\cos\dfrac{x_1} 2\cos^2\dfrac{x_2} 2+2\sin\dfrac{x_2} 2\cos\dfrac{x_2} 2\cos^2\dfrac{x_1} 2+2sin⁡2x12sin⁡x22cos⁡x22+2sin⁡x12sin⁡2x22cos⁡x12 + 2\sin^2\dfrac{x_1} 2\sin\dfrac{x_2} 2\cos\dfrac{x_2} 2+2\sin\dfrac{x_1} 2\sin^2\dfrac{x_2} 2\cos\dfrac{x_1} 2 =2sin⁡x12cos⁡x12(sin⁡2x22+cos⁡2x22)=2\sin\dfrac{x_1} 2\cos\dfrac{x_1} 2\braceNT{\sin^2\dfrac{x_2} 2+\cos^2\dfrac{x_2} 2}+2sin⁡x22cos⁡x22(sin⁡2x12+cos⁡2x12) +2\sin\dfrac{x_2} 2\cos\dfrac{x_2} 2\braceNT{\sin^2\dfrac{x_1} 2+\cos^2\dfrac{x_1} 2} =2sin⁡x12cos⁡x12+2sin⁡x22cos⁡x22=2\sin\dfrac{x_1} 2\cos\dfrac{x_1} 2+2\sin\dfrac{x_2} 2\cos\dfrac{x_2} 2 =sin⁡x1+sin⁡x2=\sin x_1+\sin x_2 □\qed
 
 

Strukturen sind die Waffen der Mathematiker.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Transzendente Funktionen