Spezielle Werte der Winkelfunktionen
Für ausgewählten Winkel lassen sich die Werte der trigonometrischen Funktionen auch als Wurzelausdrücke darstellen.
Tabelle 7CGF
| Grad | |||||
|---|---|---|---|---|---|
| Rad | |||||
| 1 | |||||
| 0 | |||||
| n.def. | |||||
| n.def. | 0 |
Herleitung
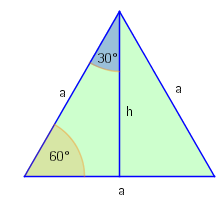
In einem gleichseitigen Dreieck finden wir die Winkel und . Es gilt nach dem Satz des Pythagoras , woraus folgt. Mit der Definition von Sinus und Kosinus erhalten wir:
und
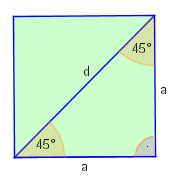
In einem Quadrat mit der Seitenlänge gilt nach dem Satz des Pythagoras für die Länge der Diagonalen . Damit erhalten wir:
.
Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.
Jakob I. Bernoulli
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе