Sekans und Kosekans
Sekans und Kosekans sind trigonometrische Funktionen.
| Sekans: | |
| Kosekans: |
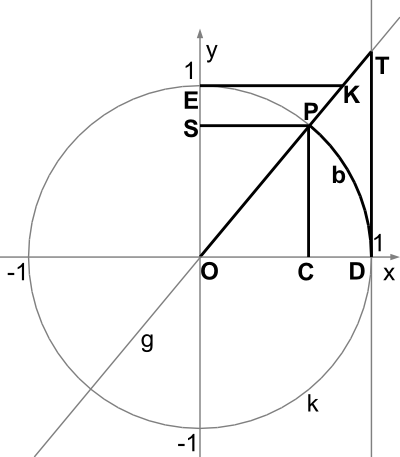
Definition am Einheitskreis
Die Funktionen haben ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge von Sekantenabschnitten:
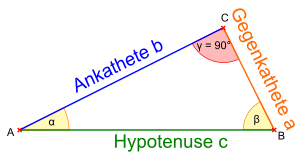
Im rechtwinkligen Dreieck ist der Sekans das Verhältnis der Hypotenuse zur Ankathete und damit die Kehrwertfunktion der Kosinusfunktion.
Der Kosekans ist das Verhältnis der Hypotenuse zur Gegenkathete und damit die Kehrwertfunktion der Sinusfunktion:
Eigenschaften
Verlauf
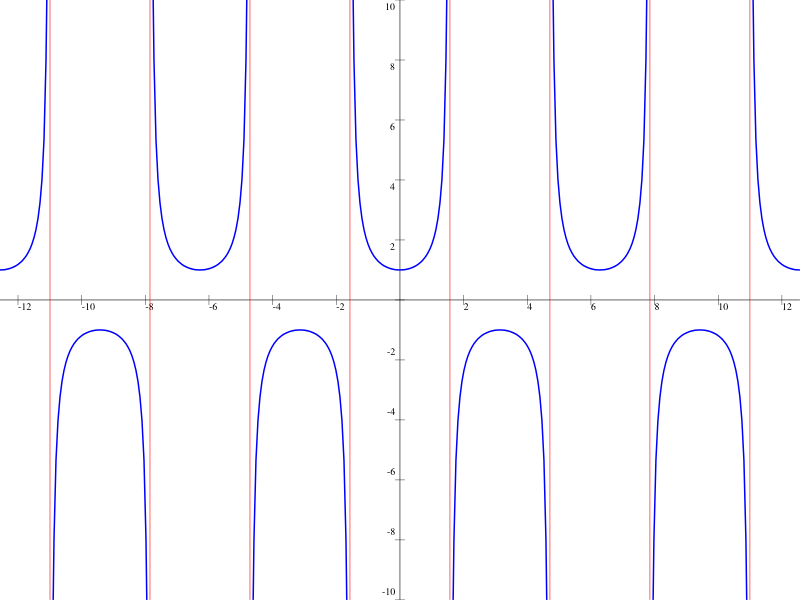
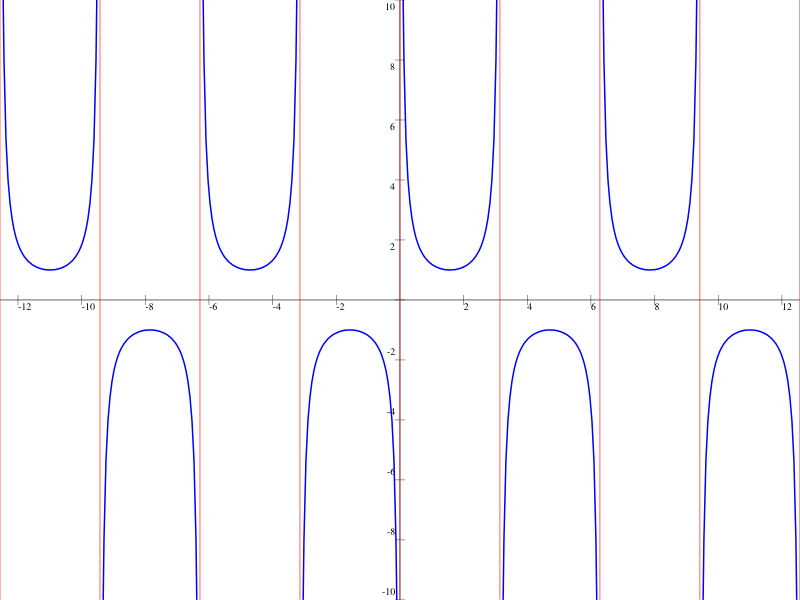
Definitionsbereich
| Sekans: | |
| Kosekans: |
Wertebereich
Periodizität
- Periodenlänge
Monotonie
- streng monoton fallende und streng monoton steigende Abschnitte.
Symmetrien
| Sekans: | Gerade Funktion: |
| Kosekans: | Ungerade Funktion: |
Polstellen
| Sekans: | |
| Kosekans: |
Extremwerte
| Sekans: | Minima: | Maxima: | ||
| Kosekans: | Minima: | Maxima: | ||
Weder die Sekansfunktion noch die Kosekansfunktion haben Asymptoten, Sprungstellen, Wendepunkte oder Nullstellen.
Umkehrfunktionen
Sekans:
- Auf einer halben Periodenlänge, z.B. ist die Funktion umkehrbar (Arkussekans):
Kosekans
- Auf einer halben Periodenlänge, z.B. ist die Funktion umkehrbar (Arkuskosekans):
Reihenentwicklung
Sekans:
Kosekans:
Ableitung
Sekans:
Kosekans
Integral
Sekans:
Kosekans
Die Furcht vor der Mathematik steht der Angst erheblich näher als der Ehrfurcht.
Felix Auerbach
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Sekans und Kosekans
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе