Gerade und ungerade Funktionen

Sei f:D→Rf:D\to \R eine reelle Funktion mit dem Definitionsbereich D⊆RD\subseteq\R.
Die Funktion ff heißt gerade, wenn für alle x∈Dx\in D gilt: f(x)=f(−x)f(x)=f(\uminus x).
Eine Funktion ff heißt ungerade, wenn für alle x∈Dx\in D gilt: f(x)=−f(−x)f(x)=-f(\uminus x) bzw. f(−x)=−f(x)f(-x)=-f(x).

Beispiele

1) f(x)=xf(x)=x ist ungerade, da f(−x)=−x=−f(x)f(\uminus x)=\uminus x=\uminus f(x) ist.
2) f(x)=x2f(x)=x^2 ist gerade, da f(−x)=(−x)2=x2=f(x)f(\uminus x)=(\uminus x)^2=x^2=f(x) ist.
3) Die Sinusfunktion f(x)=sin⁡xf(x)=\sin x ist eine ungerade Funktion; die Kosinusfunktion f(x)=cos⁡xf(x)=\cos x ist eine gerade Funktion.
 
 

Eigenschaften

Gerade und ungerade Funktion verhalten wie ihre Entsprechungen bei Zahlen. So wie das Produkt zweier gerader Zahlen wieder eine gerade Zahl ist, so ist auch das Produkt zweier gerader Funktionen gerade. Analog gilt, dass das Produkt zweier ungerader Funktionen eine gerade Funktion ergibt.
Die Summe zweier (un)gerader Funktionen ist wieder (un)gerade.
Die Ableitung einer geraden Funktion ist ungerade, die Ableitung einer ungeraden Funktion ist gerade, denn f(x)=f(−x)f(x)=f(\uminus x)   ⟹  f ′(x)=(f(−x))′=−f(−x)\implies f\, '(x)=(f(\uminus x))'=\uminus f(\uminus x) und f(x)=−f(−x)f(x)=-f(\uminus x)   ⟹  f ′(x)=(−f(−x))′=f(−x)\implies f\, '(x)=(-f(\uminus x))'=f(\uminus x).
Die Hintereinanderausführung einer

Geometrische Deutung

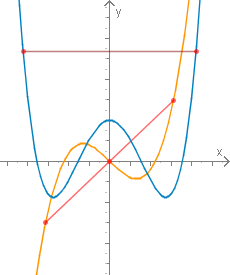
GUFunc.png
Geometrische Deutung gerader und ungerader Funktionen
Für den Graphen der Funktion ergeben sich folgende Deutungen:
Gerade Funktionen sind symmetrisch zu yy-Achse. Eine Spiegelung an der yy-Achse überführt den Graphen der Funktion in sich.
Ungerade Funktionen sind symmetrisch zum Ursprung. Eine Punktspiegelung am Ursprung überführt den Graphen der Funktion in sich.

Gerader und Ungerader Anteil einer Funktion

Sei ff eine beliebige Funktion. Wir definieren dann fg=12(f(x)+f(−x))f_g=\dfrac 1 2\left(f(x)+f(\uminus x)\right) und fu=12(f(x)−f(−x))f_u=\dfrac 1 2\left(f(x)-f(\uminus x)\right). Dann ist fgf_g eine gerade Funktion und heißt der gerade Anteil von ff. Die Funktion fuf_u ist ungerade und heißt der ungerade Anteil von ff. Weiterhin gilt f=fg+fuf=f_g+f_u; wir haben also ff in ihren geraden und ungeraden Anteil zerlegt. Dies ist für jede Funktion mit einem zum Nullpunkt symmetrischen Definitionsbereich möglich.

Beispiele

1) f(x)=x2−2x+1f(x)=x^2-2x+1 und f(−x)=x2+2x+1f(-x)=x^2+2x+1; also fg(x)=x2+1f_g(x)=x^2+1 und fu(x)=−2xf_u(x)=-2x.
2) f(x)=e⁡xf(x)=\e^x und f(−x)=e⁡−xf(\uminus x)=\e^{\uminus x}; also fg(x)=12(e⁡x+e⁡−x)=cosh⁡xf_g(x)=\dfrac 1 2(\e^x+\e^{\uminus x})=\cosh x und
fg(x)=12(e⁡x−e⁡−x)=sinh⁡xf_g(x)=\dfrac 1 2(\e^x-\e^{\uminus x})=\sinh x. Der gerade und ungerade Anteil der Exponentialfunktion sind der Hyperbelkosinus und der Hyperbelsinus.

So seltsam es auch klingen mag, die Stärke der Mathematik beruht auf dem Vermeiden jeder unnötigen Annahme und auf ihrer großartigen Einsparung an Denkarbeit.

Ernst Mach

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen