Konvexe und konkave Funktionen

In der Analysis heißt eine Funktion ff von einem Intervall II (oder allgemeiner einer konvexen Teilmenge CC eines reellen Vektorraums) nach R\mathbb{R} konvex, wenn für alle x, yx,\, y aus II (bzw. aus CC) und tt zwischen 0 und 1 gilt:
f(tx+(1−t)y)≤tf(x)+(1−t)f(y) f(t x+(1-t)y) \le t f(x)+(1-t)f(y)
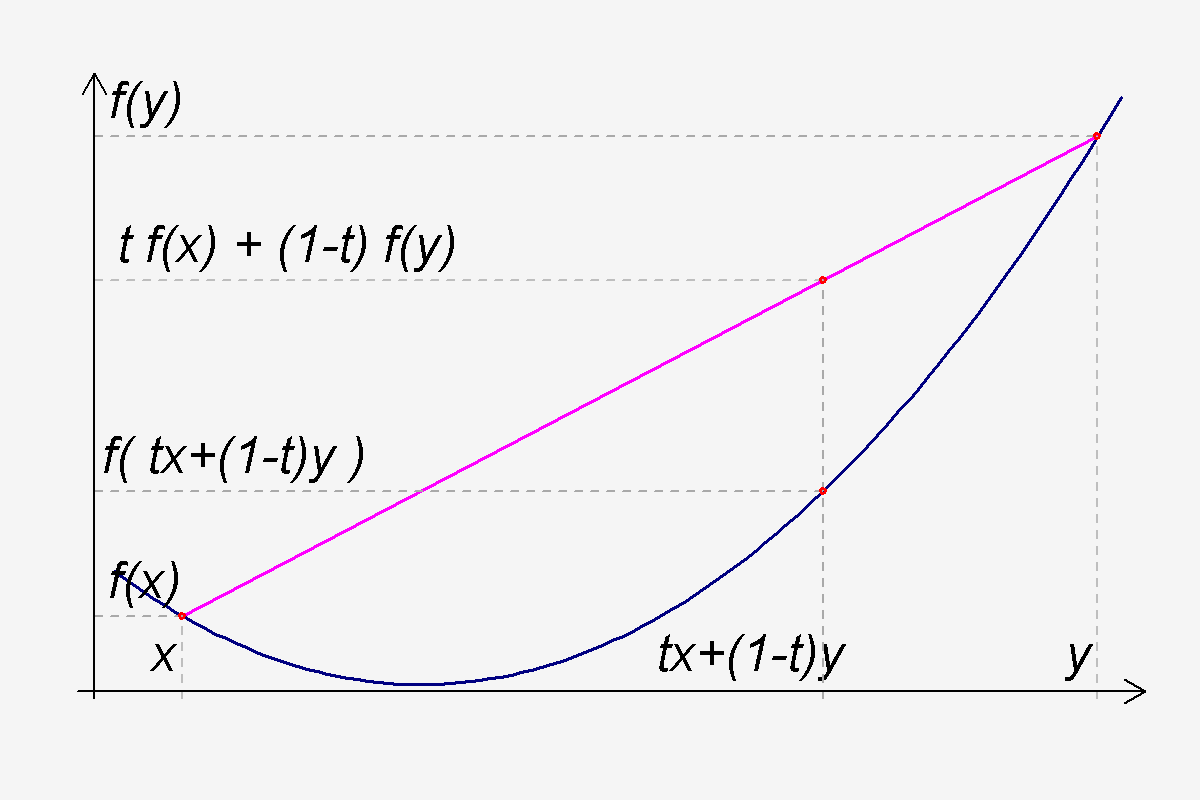
Convex_Function.png
Anschaulich bedeutet die Definition: Die Funktionswerte zwischen zwei Werten x,yx,y liegen unterhalb der Verbindungsgeraden der beiden Funktionswerte an xx und yy.
Gilt des Ungleichheitszeichen in die umgekehrte Richtung, also
f(tx+(1−t)y)≥tf(x)+(1−t)f(y) f(t x+(1-t)y) \ge t f(x)+(1-t)f(y)
für alle x, yx,\, y aus II und tt zwischen 0 und 1 gilt, so wird die Funktion als konkav bezeichnet. Vereinzelt wird der hier verwendete Begriff "konvex" als "konvex von unten" und im Gegensatz dazu "konkav" als "konvex von oben" bezeichnet.
Eine Funktion heißt streng konvex, wenn für alle x,yx,y aus II (bzw. CC) und tt echt zwischen 0 und 1 gilt:
f(tx+(1−t)y)<tf(x)+(1−t)f(y) f(t x+(1-t)y) < t f(x)+(1-t)f(y).
Analog heißt eine Funktion streng konkav, wenn für alle x,yx,y aus II (bzw. CC) und tt echt zwischen 0 und 1 gilt:
f(tx+(1−t)y)>tf(x)+(1−t)f(y) f(t x+(1-t)y) > t f(x)+(1-t)f(y).
Die besondere Bedeutung konvexer bzw. konkaver Funktionen liegt darin, dass sie allgemeiner als lineare Funktionen sind, aber einfach zu untersuchende Eigenschaften haben, die viele Aussagen über nichtlineare Systeme, insbesondere über nichtlineare Optimierungsprobleme ermöglichen.
 
 

Beispiele

Normalparabel.png
Normalparabel ist konvex

Konvexität, Beschränktheit und Stetigkeit

Schwächere Definition der Konvexität

Setzt man Stetigkeit voraus, so reicht für Konvexität in einer konvexen Teilmenge CC eines reellen topologischen Vektorraums bereits die Bedingung, dass ein beliebiges, aber fixes λ∈R\lambda\in\R mit 0<λ<10<\lambda<1 existiert, sodass für alle x,yx,y aus CC gilt:
f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)f\braceNT{\lambda x + (1-\lambda)y} \le \lambda f(x) + (1-\lambda)f(y).
Um dies zu sehen, betrachtet man die Menge TT aller "guten" tt, die durch
T={t∈[0,1]:f(tx+(1−t)y)≤tf(x)+(1−t)f(y)∀x,y∈C}T=\lbrace t \in [0,1]: f(t x+(1-t)y) \le t f(x)+(1-t)f(y) \quad \forall x,y \in C\rbrace
definiert ist.
Seien nun u,v∈Tu,v\in T. Dann gilt auch λu+(1−λ)v∈T\lambda u + \braceNT{1-\lambda}v \in T, denn
f((λu+(1−λ)v)x+(1−λu−(1−λ)v)y)f\braceNT{\braceNT{\lambda u + \braceNT{1-\lambda}v}x+\braceNT{1-\lambda u - \braceNT{1-\lambda}v}y}
=f(λ(ux+(1−u)y)+(1−λ)(vx+(1−v)y))=f\braceNT{\lambda(ux+(1-u)y)+ (1-\lambda)(vx+(1-v)y)}
≤λf(ux+(1−u)y)+(1−λ)f(vx+(1−v)y)\leq \lambda f\braceNT{ux+(1-u)y}+ (1-\lambda)f\braceNT{vx+(1-v)y}
≤λ(uf(x)+(1−u)f(y))+(1−λ)(vf(x)+(1−v)f(y))\leq \lambda \braceNT{ uf(x)+(1-u)f(y)}+ (1-\lambda)\braceNT{vf(x)+(1-v)f(y)}
=(λu+(1−λ)v)f(x)+(1−λu−(1−λ)v)f(y)=\braceNT{\lambda u + (1-\lambda)v}f(x)+ \braceNT{1- \lambda u - (1-\lambda)v} f(y).
Sein nun tt eine beliebige reelle Zahl mit 0<t<10<t<1. Dann lässt sich eine Intervallschachtelung [un,vn][u_n,v_n] mit un,vn∈Tu_n, v_n \in T konstruieren, die gegen tt konvergiert: Sei u0=0,v0=1u_0=0, v_0=1 und 0≤un≤t<vn≤10\leq u_n\leq t < v_n\leq 1 und 0<vn−un≤qn0<v_n-u_n\leq q^n mit 0<q:=min⁡(λ,1−λ)<10<q:=\min\braceNT{\lambda, 1-\lambda}<1.
Sei tn:=λun+(1−λ)vnt_n:=\lambda u_n + \braceNT{1-\lambda}v_n.
Ist tn≤tt_n\leq t, so setzt man un+1:=tn, vn+1:=vnu_{n+1}:=t_n,\, v_{n+1}:=v_n und es gilt vn+1−un+1=λ(vn−un)v_{n+1}-u_{n+1}=\lambda(v_n-u_n).
Ist tn>tt_n> t, so setzt man un+1:=un, vn+1:=tnu_{n+1}:=u_n,\, v_{n+1}:=t_n und es gilt vn+1−un+1=(1−λ)(vn−un)v_{n+1}-u_{n+1}=(1-\lambda)(v_n-u_n).
un+1,tn+1u_{n+1}, t_{n+1} sind ebenfalls aus TT, es gilt t∈[un+1,vn+1]t\in[u_{n+1}, v_{n+1}] und 0<vn+1−un+1≤qn+10<v_{n+1}-u_{n+1}\leq q^{n+1}.
Die so konstruierte Intervallschachtelung konvergiert also gegen tt; wegen der Stetigkeit von ff gilt daher t∈Tt\in T. Da tt beliebig gewählt war, folgt also T=[0,1]T=[0,1] und ff ist konvex.

Gegenbeispiel ohne Stetigkeit

Dass Stetigkeit für die schwächere Definition wirklich benötigt wird, lässt sich mit folgendem Gegenbeispiel zeigen: Ist bj∈R,j∈Jb_j \in \R, j\in J eine Hamelbasis des Vektorraums der reellen Zahlen über dem Körper der rationalen Zahlen, also eine über den rationalen Zahlen linear unabhängige Menge reeller Zahlen, in der jede reelle Zahl rr eine Darstellung der Art r=∑j∈Jqjbjr=\sum\limits_{j\in J}q_j b_j mit nur endlich vielen rationalen qj≠0q_j\neq 0 hat, so erfüllt bei beliebiger Wahl von f(bj)f(b_j) die Funktion f(r):=∑j∈Jqjf(bj)f(r):=\sum\limits_{j\in J}q_j f(b_j) zwar f(x+y2)≤f(x)+f(y)2,f\braceNT{\dfrac{x+y}{2}} \le \dfrac{f(x)+f(y)}{2}, ist aber nicht notwendigerweise konvex.

Beschränktheit und Konvexität

Setzt man für eine Funktion ff zusätzlich zur Bedingung dass für ein fixes λ∈(0,1)\lambda\in(0,1) die Beziehung
f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)f\braceNT{\lambda x + (1-\lambda)y} \le \lambda f(x) + (1-\lambda) f(y)
für alle x,yx,y aus einer konvexen Teilmenge CC eines normierten Vektorraums gilt, noch voraus, dass ff nach oben beschränkt ist, so folgt daraus bereits die Stetigkeit von ff in den inneren Punkten von CC. Anschaulich wird dies daraus klar, dass man an einer Unstetigkeitsstelle eine beliebig steile Verbindungsgerade zwischen zwei Funktionswerten ziehen kann, wobei die Funktion zwischen den beiden Werten unterhalb der Verbindungsgeraden und außerhalb der beiden Werte oberhalb der Verbindungsgerade liegen muss. Kann die Verbindungsgerade nun beliebig steil werden, so stößt man irgendwann über die obere Schranke der Funktion.
Formal ist der Beweis allerdings etwas komplizierter. Zunächst beachte man, dass aus den obigen Voraussetzungen für natürliche Zahlen nn und
x=λnu+(1−λn)yx=\lambda^n u+\braceNT{1-\lambda^n}y
folgt, dass
f(x)≤λnf(u)+(1−λn)f(y)f(x)\le \lambda^n f(u)+\braceNT{1-\lambda^n}f(y)
bzw.
f(u)=f(1λnx−(1λn−1)y)≥1λnf(x)−(1λn−1)f(y)f(u)=f\braceNT{\dfrac{1}{\lambda^n} x - \braceNT{\dfrac{1}{\lambda^n}-1}y}\geq \dfrac{1}{\lambda^n} f(x) - \braceNT{\dfrac{1}{\lambda^n}-1}f(y) .
Sei nun aa ein beliebiger innerer Punkt von CC und
Bρ(a)={x:∥x−a∥<ρ}⊆CB_\rho(a)=\lbrace x:\|x-a\|<\rho\rbrace \subseteq C
eine zur Gänze in CC enthaltene offene Kugel um aa. Wäre nun ff nicht stetig in aa, so gäbe es ein ε>0\varepsilon>0 sodass für jedes δ>0\delta>0 ein xx existiert, sodass zwar ∥a−x∥<δ\|a-x\|<\delta aber ∣f(x)−f(a)∣>ε|f(x)-f(a)|>\varepsilon. Sein nun n∈Nn\in\N so gewählt, dass
1λn−1>M−f(a)ε\dfrac{1}{\lambda^n}-1>\dfrac{M-f(a)}{\varepsilon},
wobei MM eine obere Schranke für ff sei. Wählt man nun δ=λnρ\delta=\lambda^n \rho, so existiert also ein xx mit
∥x−a∥<λnρ\|x-a\|<\lambda^n \rho
aber
∣f(x)−f(a)∣>ε|f(x)-f(a)|>\varepsilon.
Angenommen, f(x)>f(a)+ϵf(x)>f(a)+\epsilon. Dann gilt für y:=1λnx−(1λn−1)ay:=\dfrac{1}{\lambda^n}x-\braceNT{\dfrac{1}{\lambda^n}-1}a
f(y)=f(1λnx−(1λn−1)a)≥1λnf(x)−(1λn−1)f(a)>f(a)+1λnϵ>Mf(y)=f\braceNT{\dfrac{1}{\lambda^n}x-\braceNT{\dfrac{1}{\lambda^n}-1}a}\ge \dfrac{1}{\lambda^n} f(x) - \braceNT{\dfrac{1}{\lambda^n}-1}f(a)> f(a)+\dfrac{1}{\lambda^n}\epsilon > M.
Das kann aber nicht sein, da ∥y−a∥=1λn∥x−a∥<ρ\|y-a\|=\dfrac{1}{\lambda^n}\|x-a\|<\rho. Daher liegt yy in CC und es muss f(y)<Mf(y)<M gelten.
Sei daher f(x)<f(a)−ϵf(x)<f(a)-\epsilon. Dann gilt für z:=1λna−(1λn−1)xz:=\dfrac{1}{\lambda^n} a-\braceNT{\dfrac{1}{\lambda^n}-1}x
f(z)=f(1λna−(1λn−1)x)≥1λnf(a)−(1λn−1)f(x)>f(a)+(1λn−1)ϵ>Mf(z)=f\braceNT{\dfrac{1}{\lambda^n} a-\braceNT{\dfrac{1}{\lambda^n}-1}x}\ge \dfrac{1}{\lambda^n} f(a) - \braceNT{\dfrac{1}{\lambda^n}-1}f(x)> f(a)+\braceNT{\dfrac{1}{\lambda^n}-1}\epsilon > M.
Das kann aber auch nicht sein, da ∥z−a∥=(1λn−1)∥x−a∥<ρ\|z-a\|=\braceNT{\dfrac{1}{\lambda^n}-1}\|x-a\|<\rho. Daher liegt auch zz in CC und es muss ebenfalls f(z)<Mf(z)<M gelten.
ff muss daher stetig in aa sein.
Die Aussage, dass eine konvexe beschränkte Funktion stetig in den inneren Punkten ist, ist auch bedeutsam für das Lösen der Cauchyschen Funktionalgleichung
f(x+y)=f(x)+f(y)f(x+y)=f(x)+f(y)
f(1)=af(1)=a.
Aus dieser Aussage folgt nämlich, dass diese Funktionalgleichung eine eindeutige Lösung hat, wenn zusätzlich gefordert wird, dass ff beschränkt ist.

Unendlichdimensionaler Fall

Im unendlichdimensionalen Fall brauchen konvexe Funktionen nicht stetig zu sein, da es lineare (also somit auch konvexe) Funktionale gibt, die nicht stetig sind. Allerdings gilt, dass beschränkte konvexe Funktionale eines normierten Vektorraums stetig sind.

Endlichdimensionaler Fall

Innere Punkte

Konvexe Funktionen ff einer konvexen Teilmenge C des endlichdimensionalen reellen Vektorraums Rn\R^n sind stetig in den inneren Punkten. Um das zu sehen, betrachte man einen inneren Punkt a∈Ca\in C. Für diesen existiert ein Simplex Sn⊆CS_n\subseteq C mit den Eckpunkten p1,…,pn,pn+1p_1,\dots,p_n,p_{n+1}, der aa wieder als inneren Punkt enthält. Jeder Punkt x∈Snx\in S_n ist aber in der Form
x=∑j=1n+1tjpjx=\sum\limits_{j=1}^{n+1}t_jp_j
mit
∑jtj=1\sum\limits_j t_j = 1
und 0≤tj≤10\le t_j\le 1 für alle jj darstellbar. Nach der Jensenschen Ungleichung gilt nun
f(x)=f(∑j=1n+1tjpj)≤∑j=1n+1tjf(pj)≤max⁡f(pj)=:Mf(x)=f\braceNT{\sum\limits_{j=1}^{n+1}t_jp_j}\le\sum\limits_{j=1}^{n+1}t_j f(p_j)\le\max f(p_j)=:M.
ff ist daher nach oben beschränkt und somit, wie oben gezeigt wurde, stetig im inneren Punkt aa.

Randpunkte

In Randpunkten können konvexe Funktionen unstetig sein, wie das Beispiel der Funktion [0,∞)→R[0,\infty)\to \R mit
f(x)={1fallsx=00sonst f(x)=\begin{cases}1 \qquad \textrm{falls} \quad x=0 \\ 0 \qquad \textrm{sonst}\end{cases}
zeigt, die zwar konvex ist, aber am Randpunkt x=0x=0 eine Unstetigkeit aufweist.

Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.

Bertrand Russell

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Konvexe und konkave Funktionen aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen