Betrags- und Signumsfunktion
Betragsfunktion
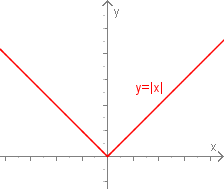
Betragsfunktion
Die Betragsfunktion ordnet jeder reellen Zahl ihren Absolutbetrag zu und ist für alle reelle Zahlen definiert. Sie nimmt nur Werte aus dem Intervall an.
Sie ist wegen eine gerade Funktion.
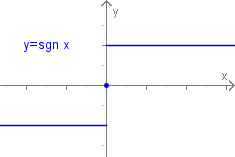
Signumsfunktion
An der Stelle ist die Signumsfunktion nicht stetig, also auch nicht differenzierbar. Für gilt , man kann also die Signumsfunktion als Ableitung der Betragsfunktion auffassen.
Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.
Leonardo da Vinci
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе