Zusammenhang von Differenzierbarkeit und Stetigkeit

Es zeigt sich, dass aus der Differenzierbarkeit einer Funktion ihre Stetigkeit folgt, umgekehrt muss jedoch eine stetige Funktion nicht differenzierbar sein.

Satz 15J3 (Stetigkeit differenzierbarer Funktionen)

Wenn eine Funktion ff in x0x_0 differenzierbar ist, so ist ff dort auch stetig.

Beweis

Nach Satz 15VC gilt:
f(x)=f(x0)+f ′(x0)⋅(x−x0)+R(x)⋅(x−x0)f(x)=f(x_0)+f\, '(x_0)\cdot(x-x_0)+R(x)\cdot(x-x_0)
mit lim⁡x→x0R(x)=0\lim_{x\rightarrow x_0}R(x)=0.
Dann ist
lim⁡x→x0f(x)\lim_{x\rightarrow x_0}f(x) =lim⁡x→x0(f(x0)+f ′(x0)⋅(x−x0)+R(x)⋅(x−x0))=f(x0)=\lim_{x\rightarrow x_0}\braceNT{f(x_0)+f\, '(x_0)\cdot(x-x_0)+R(x)\cdot(x-x_0)}=f(x_0),
und nach Satz 5225F ist ff an der Stelle x0x_0 stetig. □\qed
Die Umkehrung von Satz 15J3 muss nicht gelten, wie die folgenden Beispiele verdeutlichen.
 
 

Beispiele für stetige, nicht differenzierbare Funktionen

Beispiel 166A (Betragsfunktion)

Die Betragsfunktion ist an der Stelle x0=0x_0=0 stetig, aber nicht differenzierbar. Der Differenzenquotient hat die Form:
ΔyΔx=f(x)−f(x0)x−x0=∣x∣x\dfrac {\Delta y}{\Delta x}=\dfrac { f(x)-f(x_0)} {x-x_0}= \dfrac {|x|} x.
Er nimmt für x>0x>0 den Wert 1 und für x<0x<0 den Wert -1 an. Damit kann sein Grenzwert für x→0x\rightarrow 0 nicht existieren und die Funktion ist an dieser Stelle nicht ableitbar.
Noch unübersichtlicher ist die Situation in folgendem Beispiel.
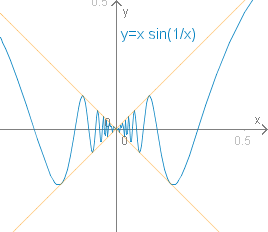
xsin1durchx.png
In Beispiel 15J5 hatten wir gezeigt, dass
lim⁡x→0x⋅sin⁡1x=0\lim_{x\rightarrow 0}x\cdot \sin\dfrac 1 x=0
gilt. Wenn man nun eine Funktion mit f(0)=0f(0)=0 und f(x)=x⋅sin⁡1xf(x)=x\cdot \sin\dfrac 1 x für x≠0x\neq0 definiert, so ist diese an der Stelle x0=0x_0=0 sicher stetig (Funktionsgrenzwert stimmt mit Funktionswert überein!) Für den Differenzenquotienten gilt:
f(0+h)−f(0)h=f(h)h=sin⁡1h\dfrac {f(0+h)-f(0)} h =\dfrac {f(h)} h= \sin\dfrac 1 h
Dieser Ausdruck hat für h→0h\rightarrow 0 keinen Grenzwert sondern oszilliert heftigst.
Die Stetigkeit einer differenzierbaren Funktion ist nicht damit zu verwechseln, dass die Ableitung als Funktion betrachtet stetig ist. Dies muss nicht notwendigerweise der Fall sein.
Wir betrachten die durch f(0)=0f(0)=0 und f(x)=x2⋅sin⁡1xf(x)=x^2\cdot \sin\dfrac 1 x für x≠0x\neq0 definierte Funktion.
ff ist differenzierbar. Für x≠0x\neq 0 können wir ihre Ableitung nach den bekannten Regeln mit
f ′(x)=2x⋅sin⁡1x−cos⁡1xf\, '(x)=2 x\cdot\sin\dfrac 1 x -\cos\dfrac 1 x
berechnen.
Für x=0x=0 müssen wir zur Definition der Ableitung greifen:
f ′(0)=lim⁡h→0f(0+h)−f(0)hf\, '(0)=\lim_{h\rightarrow 0}\dfrac {f(0+h)-f(0)} h =lim⁡h→0h2sin⁡1hh=\lim_{h\rightarrow 0} \dfrac {h^2\sin\dfrac 1 h} h =lim⁡h→0h⋅sin⁡1h=0=\lim_{h\rightarrow 0}h\cdot\sin\dfrac 1 h=0 (siehe Beispiel 15J5)
Damit existiert die Ableitung auch für x=0x=0. Die Funktion f ′(x)f\, '(x) strebt für x→0x\rightarrow 0 jedoch gegen keine Grenzwert, da dies am Term cos⁡1x\cos\dfrac 1 x scheitert.
Damit ist die Ableitung für x=0x=0 unstetig.

Wer die erhabene Weisheit der Mathematik tadelt, nährt sich von Verwirrung.

Leonardo da Vinci

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen