Taylorreihen
Satz 16K4 (Potenzreihendarstellung von Polynomen)
Sei
p(x)=k=0∑nakxk ein
Polynom n -ten Grades. Dann gilt:
p(x)=k=0∑nk!p(k)(x0)(x−x0)k
Beweis
1. Fall: Sei
x0=0.
p′(x)=a1+2a2x+⋯+nanxn−1;
p′′(x)=2a2+⋯+n(n−1)anxn−2; ...
p(k)(x)=k!ak+⋯+n(n−1)(n−k+1)anxn−k Also
p(k)(0)=k!ak für
0≤k≤n p(k)(0)=0 für
k≥n+1 ⇒p(x)=k−0∑nk!p(k)(0)xk
2. Fall: Sei
x0 beliebig. Man setze
q(y):=p(y+x0). Es gilt
q(k)(y)=p(k)(y+x0),
q(k)(0)=p(k)(x0).
p(y+x0)=q(y)=k=0∑nk!q(k)(0)yk=k=0∑nk!p(k)(x0)yk Die Substitution
y:=x−x0 ergibt
p(x)=k=0∑nk!p(k)(x0)(x−x0)k □
Sei
f eine
n -mal
stetig differenzierbare Funktion in
x0. Wegen
Satz 16K4 liegt es nahe, den Ausdruck
k=0∑nk!f(k)(x0)(x−x0)k
zur
Approximation von
f in der
Nähe von
x0 zu verwenden.
Definitionen
Sei
I⊂R ein
Intervall und
f:I→R in
x0∈I eine
n-mal
differenzierbare Funktion. Dann heißt:
Tn(f;x0):R→R
definiert durch
Tn(f;x0):=k=0∑nk!f(k)(x0)(x−x0)k
n-tes
Taylorpolynom von
f im Punkt
x0.
Sei
f:I→R beliebig oft
differenzierbar in
x∈I. Dann heißt
T(f;x0)(x):=k=0∑∞k!f(k)(x0)(x−x0)k
Taylorreihe von
f in
x mit Entwicklungspunkt
x0. Gilt für eine
unendlich oft
differenzierbare Funktion f:I→R in
x0∈I:
f(x)=k=0∑∞k!f(k)(x0)(x−x0)k , so sagt man,
f ist in
I eine
Taylorreihe entwickelbar mit dem Entwicklungspunkt
x0.
Rn(f;x0)=f−Tn(f;x0) oder kürzer
Rn heißt
Restglied.
f:I→R in
x0 genau dann taylorentwickelbar, wenn
limn→∞Rn(x)=0 Bei einem Spezialfall der
Taylorreihe mit Entwicklungspunkt 0 spricht man auch von der
MacLaurinschen Reihe.
Beispiele
Exponentialfunktion
f(x)=ex,
x0∈R beliebig.
f(k)(x0)=ex0.
f(x)=ex=ex0ex−x0 =ex0k=0∑∞k!(x−x0)k =k=0∑∞k!ex0(x−x0)k =k=0∑∞k!f(k)(x0)(x−x0)k. Also ist
f(x)=ex für
x0∈R taylorentwickelbar.
Eine nicht taylorentwickelbare Funktion
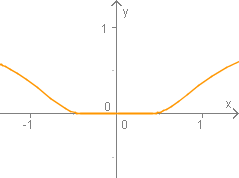
f ist für
x0=0 nicht taylorentwickelbar
f(x)=⎩⎪⎨⎪⎧e−x210x=/0x=0 Es gilt
f(k)(0)=0 für
k=0,1,2,…. Somit ist
T(f;x0=0)=k=0∑∞k!f(k)(0)xk=0. Aber
f(x)=/0 für
x=/0. Damit ist
f in
x0=0 nicht taylorentwickelbar.
Eine Funktion, die sehr schlecht durch die Taylorreihe approximiert wird
Die
Taylorreihe einer
Funktion konvergiert nicht immer gegen die
Funktion. Im folgenden Beispiel stimmt die
Taylorreihe auf keiner
Umgebung um den Entwicklungspunkt mit der Ausgangsfunktion überein:
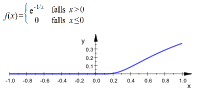
f(x)={e−1/x0fallsfallsx>0x≤0
Als
reelle Funktion ist
f unendlich oft
stetig differenzierbar, wobei die
Ableitungen in jedem Punkt
x≤0 (insbesondere für
x=0) ausnahmslos 0 sind. Die
Taylorreihe um den Nullpunkt ist also die Nullfunktion, und stimmt in keiner
Umgebung der 0 mit
f überein. Die
Taylorreihe um einen Punkt
a>0 konvergiert zwischen 0 und
2a gegen
f.
Wie ist es möglich, daß die Mathematik, letztlich doch ein Produkt menschlichen Denkens unabhängig von der Erfahrung, den wirklichen Gegebenheiten so wunderbar entspricht?
Albert Einstein
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе