Bernoulli-Zahlen

Die Bernoulli-Zahlen $B_{n}$ sind eine Folge rationaler Zahlen, die in der Mathematik in verschiedenen Zusammenhängen auftreten: als Entwicklungskoeffizienten trigonometrischer, hyperbolischer und anderer Funktionen, in der Euler-Maclaurin-Formel, und in der Zahlentheorie in Zusammenhang mit der riemannschen Zetafunktion. Die Benennung dieser Zahlen nach ihrem Entdecker Johann Bernoulli wurde von Abraham de Moivre eingeführt.

Achtung: In der Literatur werden die Bernoulli-Zahlen in zwei verschiedenen Weisen definiert. Zur Unterscheidung schreiben wir $B_{n}$ für die in Kontinentaleuropa üblichere Variante und $ß_{n}$ für die abweichende Variante.

Die Bernoulli-Zahlen werden am einfachsten als Taylor-Koeffizienten der erzeugenden Funktion $x/(e^{x} - 1)$ eingeführt. Die Reihenentwicklung

beziehungsweise

konvergiert für alle $x$ mit einem Betrag kleiner als $2p$.

Die ersten Bernoulli-Zahlen lauten $B_{1}$, $B_{2}$, $B_{3}$, ... = 1/6, 1/30, 1/42, 1/30, 5/66, 691/2730, 7/6, 3617/510, 43867/798, 174611/330, 854513/138, ... Diese Zahlen finden sich beispielsweise in der Reihenentwicklung des Tangens, Tangens Hyperbolicus oder Cosecans wieder.

In der alternativen Definition ist $ß_{1}$=-1/2, alle weiteren $ß$ mit ungeradem Koeffizienten verschwinden: $ß_{2n+1}$=0. Die ß mit geraden Koeffizienten ergeben sich aus den $B_{n}$ gemäß

als $ß_{2}$, $ß_{4}$, $ß_{6}$, ... = 1/6, -1/30, 1/42, -1/30, 5/66, ...

Die folgenden Reihenentwicklungen liefern die klassischen (im o.g. Sinne) Bernoulli-Zahlen:

$B_n = \dfrac{ (2n)!} {2^{2n - 1}\pi ^ {2n}} \cdot \sum\limits_{k=1}^\infty \dfrac{1}{ k^{2n}}$

$B_n = \dfrac{ 2 \cdot (2n)!} {(2^{2n} - 1)\cdot\pi ^ {2n}} \cdot \sum\limits_{k=0}^\infty \dfrac{1}{ (2k + 1) ^{2n}}$

$B_n = \dfrac{(2n)!} {(2^{2n - 1} - 1)\cdot\pi ^ {2n}} \cdot \sum\limits_{k=1}^\infty \dfrac{(-1)^{k-1}}{ k^{2n}}$

Die Bernoulli-Polynome sind eine Abbildung $B_k:[0,1] \rightarrow \mathbb{R}$ und sind durch folgende Rekursionsgleichungen vollständig charakterisiert:

$\, B_0(x) = 1$

und

$B'_k(x) = k \cdot B_{k-1}(x)$ mit der Nebenbedingung $\int\limits_0^1 B_k(x) \, \d x = 0$

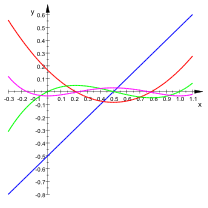
Die ersten vier Polynome lauten etwa:

$B_1(x) = x-\dfrac{1}{2}$ (blau)

$B_2(x) = x^2 - x + \dfrac{1}{6}$ (rot)

$B_3(x) = x^3 -\dfrac{3}{2}x^2 +\dfrac{1}{2}x$ (grün)

$B_4(x) = x^4 -2x^3 + x^2 -\dfrac{1}{30}$ (lila)

Die konstanten Terme dieser Polynome stehen in direktem Zusammenhang mit den Bernoulli-Zahlen, denn es sind gerade die Bernoulli-Zahlen $\beta_n$.