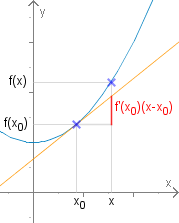
Ableitung als Linearisierung

Differenzieren bedeutet Linearisieren. Die Ableitung ist nichts anderes als der Anstieg der Tangente und mit dem folgenden Satz die lineare Funktion, die die ursprüngliche Funktion am besten annähert.

Satz 15VC

Wenn für eine Funktion ff an der Stelle x0x_0 die Ableitung f ′(x0)f\, '(x_0) existiert, dann ist
f(x)=f(x0)+f′(x0)⋅(x−x0)f(x)=f(x_0)+f'(x_0)\cdot(x-x_0) +R(x)⋅(x−x0)+R(x)\cdot(x-x_0),
wobei lim⁡x→x0R(x)=0\lim_{x\rightarrow x_0}R(x)=0 gilt.
AblLin.png
Für Werte nahe 00 kann man den Wert von R(x)R(x) vernachlässigen und der Term für f(x)f(x) ist eine Geradengleichung.
 
 

Beweis

Wir wählen R(x)=f(x)−f(x0)x−x0−f´(x0)R(x)=\dfrac {f(x)-f(x_0)}{x-x_0} -f´(x_0) für x≠x0x\neq x_0 und R(x0)=0R(x_0)=0. Dann ist wegen der Definition der Ableitung lim⁡x→x0R(x)=0\lim_{x\rightarrow x_0}R(x)=0.
Es gilt dann:
f(x0)+f´(x0)⋅(x−x0)+(f(x)−f(x0)x−x0−f´(x0))⋅(x−x0)=f(x)f(x_0)+f´(x_0)\cdot(x-x_0)+\braceNT{\dfrac {f(x)-f(x_0)}{x-x_0} -f´(x_0)}\cdot(x-x_0)=f(x).
□\qed

Beispiel

Für die Funktion f(x)=sin⁡xf(x)=\sin x wollen wir eine Näherung für x0=0x_0=0 ermitteln. Es ist f ′(x)=cos⁡xf\, '(x)=\cos x (Satz 5317E) und damit gilt:
f(x)≈sin⁡0+cos⁡0(x−0)=xf(x)\approx \sin 0 +\cos 0(x-0)= x.
Es gilt sin⁡(0,1)≈0,09983≈0,1\sin (0,1)\approx 0,09983\approx 0,1, womit die Näherung für kleine xx sehr gut zu sein scheint.

Strukturen sind die Waffen der Mathematiker.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen