Lineare Funktionen

Eine lineare Funktion ist ein Polynom vom Grad 1.
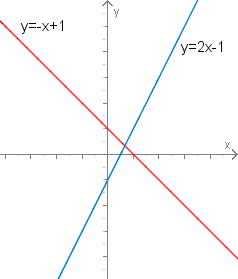
lin.png
Zwei lineare Funktionen (Geraden)
Lineare Funktionen werden in der Form
y=f(x)=mx+ny=f(x)=mx+n
für m,n∈Rm,n\in \dom R, m≠0m\neq 0 geschrieben. Der Wert mm heißt Anstieg der Funktion.
Der Graph einer linearen Funktion ist eine Gerade. Für m>0m>0 ist die Funktion monoton wachsend und für m<0m<0 monoton fallend.
Die yy-Achse wird an der Stelle y0=ny_0=n geschnitten.
Einzige Nullstelle ist x0=−nmx_0=-\dfrac { n}{m}.

Geradengleichung durch zwei Punkte

Sind zwei Punkte (x1,y1)(x_1,y_1) und (x2;y2)(x_2;y_2) gegeben mit x1!=x2x_1!=x_2, so beschreiben diese eindeutig eine lineare Funktion. Zum Bestimmen der Parameter mm und nn müssen wir das lineare Gleichungssystem
y1=mx1+ny_1=mx_1+n
y2=mx2+ny_2=mx_2+n
lösen. Es ergeben sich m=y2−y1x2−x1m=\dfrac{y_2-y_1}{x_2-x_1} und n=y1−y2−y1x2−x1⋅x1n=y_1-\dfrac{y_2-y_1}{x_2-x_1}\cdot x_1 =y1x2−y2x1x2−x1=\dfrac{y_1x_2-y_2x_1}{x_2-x_1}.

Beispiel

Gesucht ist die Geradengleichung für die lineare Funktion durch P1=(1;1)P_1=(1;1) und P2=(3;5)P_2=(3;5). Das Gleichungssystem lautet:
1=1⋅m+n1=1\cdot m+n
5=3⋅m+n5=3\cdot m+n
  ⟹  2m=4\implies 2m=4   ⟹  m=2\implies m=2. Einsetzen ergibt 1=2+n1=2+n   ⟹  n=−1\implies n=\me. (Für den Graphen siehe obige [!Abbildung].)
 
 

Nach unserer bisherigen Erfahrung sind wir zum Vertrauen berechtigt, dass die Natur die Realisierung des mathematisch denkbar Einfachsten ist.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen