Rationale Funktionen

Eine Funktion ff ist genau dann eine rationale Funktion, wenn sie sich als Quotient zweier Polynome gg und hh darstellen lässt:
f(x)=g(x)h(x)=∑i=0naixi∑j=0mbjxjf(x)=\dfrac {g(x)}{h(x)} =\dfrac {\sum\limits_{i=0}^n {a_ix^i} } {\sum\limits_{j=0}^m {b_jx^j} }
mit m,n∈Nm,n\in \dom N und bm≠0b_m\neq 0.
Die rationalen Funktionen werden auch gebrochen rationale Funktionen genannt in Unterscheidung zu den ganzrationalen Funktionen.
 
 

Beispiele

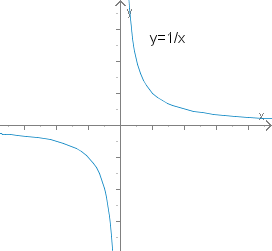
1DurchX.png
Einheitshyperbel
1) f(x)=1xf(x)=\dfrac 1 x ist eine einfache rationale Funktion, die Einheitshyperbel.
2) f(x)=2x2+1x−7f(x)=\dfrac {\sqrt 2 x^2+1} {x- \sqrt 7} zeigt, dass auch irrationale Zahlen als Koeffizienten in rationalen Funktionen auftreten dürfen.

Echt gebrochen rationale Funktionen

Eine rationale Funktion heißt eine echt gebrochen rationale Funktion, wenn der Grad des Nennerpolynoms größer ist als der des Zählerpolynoms; andernfalls heißt die Funktion unecht gebrochen rational.
Beispiel 1) war eine echt rationale Funktion; Beispiel 2) eine unecht gebrochene rationale Funktion.
Jede unecht gebrochene rationale Funktion kann mittels Polynomdivision als Summe eines Polynoms und einer echt gebrochenen rationalen Funktion dargestellt werden.

Beispiel

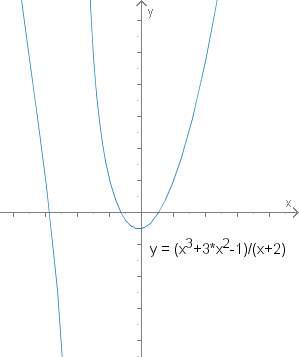
br2.png
f(x)=x3+3x2−1x+2f(x)=\dfrac{x^3+3x^2-1}{x+2} ist unecht gebrochen. Nach der Polynomdivision von Zähler durch Nenner erhalten wir: f(x)=x2+x−2+3x+2f(x)=x^2+x-2+\dfrac 3 {x+2}.

Normalform rationaler Funktionen

Wenn f(x)=g(x)h(x)f(x)=\dfrac {g(x)} {h(x)} eine rationale Funktion ist und die beiden Polynome g(x)g(x) und h(x)h(x) gemeinsame Nullstellen x01…x0kx_{0_1}\ldots x_{0_k} haben, dann kann man ff in folgender Form schreiben:
f(x)=(x−x01)⋅…⋅(x−x0k)g‾(x)(x−x01)⋅…⋅(x−x0k)h‾(x)f(x)=\dfrac {\braceNT{x-x_{0_1}}\cdot\ldots\cdot\braceNT{x-x_{0_k}} \overline g(x) } {\braceNT{x-x_{0_1}}\cdot\ldots\cdot\braceNT{x-x_{0_k}} \overline h(x)},
dabei haben g‾(x)\overline g(x) und h‾(x)\overline h(x) keine gemeinsamen Nullstellen mehr.
Die rationale Funktion f‾(x)=g‾(x)h‾(x)\overline f(x)=\dfrac {\overline g(x)}{\overline h(x)} stimmt bis auf ihr Verhalten an den gemeinsamen Nullstellen von gg und hh mit ff überein und heißt Normalform.
Es gilt sogar:
f‾(x0l )=lim⁡x→x0lf(x)\overline f(x_{0_l}\, )=\lim_{x\rightarrow x_{0_l}} f(x) für l=1…kl=1\ldots k

Seit der Zeit der Griechen bedeutet "Mathematik" zu sagen, "Beweis" zu sagen.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Reelle Funktionen