Asymptotisches Verhalten rationaler Funktionen

Sei f(x)=azxz+az−1xz−1+⋯+a1x+a0bnxn+bn−1xn−1+⋯+b1x+b0=g(x)h(x) f(x)=\dfrac{a_z x^z+a_{z-1} x^{z-1}+\cdots +a_1x+a_0}{b_n x^n+b_{n-1} x^{n-1}+\cdots +b_1x+b_0} = \dfrac{g(x)}{h(x)} eine rationale Funktion.
Für das Verhalten für xx gegen Unendlich sind die Grade zz bzw. nn des Zähler- bzw. Nenner-Polynoms entscheidend:
Für x→∞x\to\infty geht f(x)f(x)
  • gegen sgn⁡(azbn)⋅∞\sgn\left(\dfrac{a_z}{b_n}\right)\cdot\infty, falls z>nz>n, wobei mit "sgn" das Vorzeichen des Quotienten gemeint ist (siehe Signum),
  • gegen azbn\dfrac{a_z}{b_n}, falls z=nz=n (die Asymptote ist parallel zur x-Achse),
  • gegen 00 (die x-Achse ist waagrechte Asymptote), falls z<nz<n,
Für x→−∞x\to -\infty ergibt sich im zweiten und dritten Fall jeweils derselbe Grenzwert wie für x→∞x \to \infty. Im ersten Fall muss man Zähler- und Nennergrad noch genauer berücksichtigen:
  • Ist z−nz - n gerade, so ergibt sich derselbe Grenzwert wie für x→∞x \to \infty.
  • Ist z−nz - n ungerade, so ändert sich im Vergleich zu x→∞x \to \infty das Vorzeichen des Grenzwerts.
Wie weiter unten beschrieben, kann man im ersten Fall den Funktionsterm mittels Polynomdivision immer in ein Polynom und einen echt gebrochenrationalen Term zerlegen; das Polynom beschreibt dann eine sogenannte Asymptotenkurve. (Das Verhalten der Funktionswerte für x→±∞x \to \pm \infty kann man dann auch einfacher erhalten, indem man nur das Verhalten der Asymptotenkurve untersucht.) Im Sonderfall z=n+1z=n+1 ergibt sich eine schräg verlaufende Asymptote.

Asymptote

Durch die Polynomdivision von gg durch hh erhält man g=a⋅q+rg = a\cdot q + r mit Polynomen aa und rr, wobei der Grad von rr kleiner als der von hh ist. Das asymptotische Verhalten von
f=(gh)=a+(rh)f = \over{g}{ h} = a + \over{r}{ h}
ist damit durch die ganzrationale Funktion ("Asymptotenfunktion") aa bestimmt.
  1. z<n→z < n \to x-Achse ist Asymptote: a(x)=0a(x) = 0
  2. z=n→z = n \to waagerechte Asymptote: a(x)=azbna(x) = \dfrac{a_z}{b_n}
  3. z=n+1→z = n + 1 \to schräge Asymptote: a(x)=mx+c ;m≠0a(x) = mx + c \,; m \ne 0 (Spezialfall von 4)
  4. z>n+1→z > n +1 \to polynomiale Näherungsfunktion

Beispiele

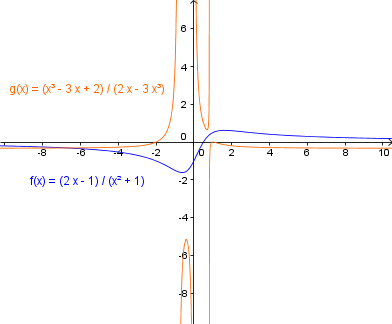
405_asym1.png
Bei der gebrochenrationalen Funktion f:x↦2x−1x2+1f: x \mapsto \dfrac{2x - 1}{x^2 + 1} ist der Zählergrad zz = 1 und der Nennergrad nn = 2, der Grenzwert für x→±∞x \to \pm \infty ist also 00.
Die gebrochenrationale Funktion g:x↦x3−3x+22x−3x3g: x \mapsto \dfrac{x^3 - 3x + 2}{2x - 3x^3} hat den Zählergrad zz = 3 und auch den Nennergrad nn = 3; da hier a3=1a_3 = 1 und b3=−3b_3 = -3 ist, ergibt sich für die Gleichung der waagrechten Asymptote: y=−13y = -\dfrac{1}{3}.
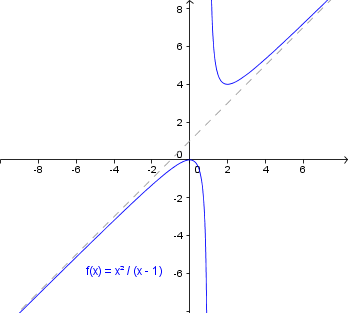
407_asym2.png
Die gebrochenrationale Funktion f:x↦x2x−1f: x \mapsto \dfrac{x^2}{x-1} hat den Zählergrad zz = 2 und den Nennergrad nn = 1; mit den Koeffizienten a2=1a_2 = 1 und b1=1b_1 = 1 ergibt sich also: f(x)→sgn⁡(11)⋅∞=+∞f(x) \to \sgn\left(\dfrac{1}{1}\right)\cdot\infty = +\infty für x→∞x \to \infty. Da hier z−n=1z - n = 1 ungerade ist, folgt für den Grenzwert für x→−∞x \to -\infty das umgedrehte Vorzeichen, also f(x)→−∞f(x) \to -\infty. Diese Funktion kann man auch schreiben als f:x↦x+1+1x−1f: x \mapsto x + 1 + \dfrac{1}{x-1}, das heißt, die (schräge) Asymptote hat die Gleichung y=x+1y = x + 1 (und daraus ergibt sich auch leicht wieder das eben geschilderte Grenzverhalten).
 
 

Wir Mathematiker sind die wahren Dichter, nur müssen wir das, was unsere Phantasie schafft, noch beweisen.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Rationale Funktion aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen