Wurzelfunktionen

Die Wurzelfunktion

ist die Umkehrfunktion zur Potenzfunktion $y=x^n$.

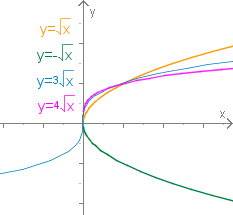
Ist $n$ gerade so ist die Potenzfunktion nicht injektiv und daher nicht eindeutig umkehrbar. Es gibt es zwei Möglichkeiten die Wurzelfunktion zu definieren $f(x)=\sqrtN n x$ und $f(x)=-\sqrtN n x$. Dabei wird im Allgemeinen die positive Variante als die Umkehrfunktion angesehen.

Falls $n$ ungerade ist, so ist die Wurzelfunktion auf ganz $\R$ umkehrbar.

Falls $n$ gerade betrachten wir nur den positiven Zweig.

Die Wurzelfunktion ist streng monoton wachsend und wächst unbeschränkt für $x\to\infty$.

Für $n$ ungerade handelt es sich wegen $\sqrtN n {-x}=-\sqrtN n x$ um eine ungerade Funktion.

Die einzige Nullstelle liegt bei $x_0=0$.

Weiterhin gelten die folgenden Grenzwerte:

$\lim_{n\rightarrow\infty}\sqrt[n]{a}= 1$ für $a > 0$ $\lim_{n\rightarrow\infty}\sqrt[n]{n}= 1$