Potenzfunktion

Die Potenzfunktion y=xny=x^n, n∈Nn\in \dom N ist ein Polynom vom Grade nn.
Es sind zwei Fälle zu unterscheiden.
Die einzige Nullstelle der Potenzfunktion ist x0=0x_0=0.
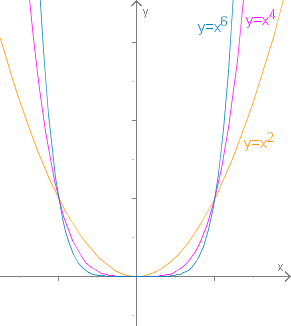
xng.png
Potenzfunktionen mit geraden Exponenten

Fall 1: nn ist gerade

Dann gilt für ein n=2kn=2k: (−x)2k=((−x)2)k=x2k(\uminus x)^{2k}=((\uminus x)^{2})^{k}=x^{2k}. Damit ist die Funktion in diesem Fall gerade.
Sie ist streng monoton fallend im Intervall ]−∞,0]]\uminus\infty,0] und streng monoton wachsend im Intervall [0,∞[[0,\infty[.
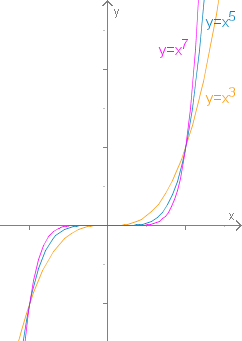
xnu.png
Potenzfunktionen mit ungeraden Exponenten

Fall 2: nn ist ungerade

Dann ist auch die Potenzfunktion ungerade.
Sie ist streng monoton wachsend für alle x∈Rx\in \dom R.
 
 

Es gibt jedoch noch einen anderen Grund für die hohe Wertschätzung der Mathematik; sie allein bietet den Naturwissenschaften ein gewisses Maß an Sicherheit, das ohne Mathematik nicht erreichbar wäre.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen