Quadratische Funktionen

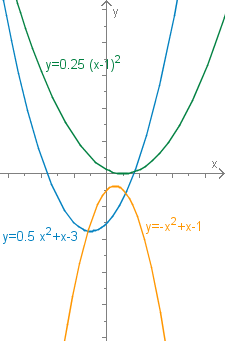
quad.png
Verschiedene quadratische Funktionen
Eine quadratische Funktion ist ein Polynom vom Grad 2.
Die allgemeine Form ist
y=f(x)=ax2+bx+cy=f(x)=ax^2+bx+c,
wobei a≠0a\neq 0 vorausgesetzt wird, da die Funktion sonst zu einer linearen Funktion entartet.
Der Graph der Funktion ist eine Parabel, die für a>0a>0 nach oben geöffnet ist und für a<0a<0 nach unten (siehe Grafik).
Der Scheitelpunkt SS hat die Koordinaten (−b2a; c−b24a)\braceNT{-\dfrac b {2a};\, c-\dfrac {b^2}{4a}}.
Die Normalparabel y=x2y=x^2 ist eine gerade Funktion.

Nullstellen

Je nach Lösungsverhalten der zugehörigen quadratischen Gleichung hat die Funktion keine, eine oder zwei Nullstellen. Wenn die Funktion eine Nullstelle hat, liegt der Scheitelpunkt auf der xx-Achse.
 
 

Seit die Mathematiker über die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr.

Albert Einstein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Klassen von Funktionen