Parabel

Die Parabel ist diejenige Menge von Punkten der Ebene, die zu einer Linie und einem Punkt den gleichen Abstand haben.
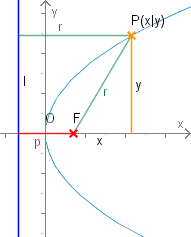
Parabel.png
Um die Gleichung der Parabel herzuleiten, legen wir den Ursprung in die Mitte der Lotstrecke zwischen Brennpunkt FF und Gerade ll. Sei pp der Abstand von FF und ll.
Dann nimmt die Gleichung der Parabel folgende Form an:

Formel 15VV (Gleichung der Parabel in Normalform)

y2=2pxy^2=2px

Herleitung

Es gilt einerseits r=x+p2r=x+\dfrac p 2 und andererseits nach dem Satz des Pythagoras r2=(x−p2)2+y2r^2={\braceNT{x-\dfrac p 2}}^2+y^2. Quadrieren wir die erste Gleichung und setzen dann beide gleich, erhalten wir:
(x+p2)2=(x−p2)2+y2{\braceNT{x+\dfrac p 2}}^2={\braceNT{x-\dfrac p 2}}^2+y^2
  ⟹  x2+px+p24=x2−px+p24+y2\implies x^2+px+\dfrac {p^2} 4=x^2-px+\dfrac {p^2} 4+y^2   ⟹  y2=2px\implies y^2=2px. □\qed

Gleichung in Polarkoordinaten

Die Gleichung der Parabel in Polarkoordinaten lautet
r=p1+cos⁡φr=\dfrac p{1+\cos\phi}
Dies entspricht der Gleichung der anderen Kurven 2.Ordnung
r=p1+ϵcos⁡φr=\dfrac p{1+\epsilon\cos\phi}
mit ϵ=1\epsilon=1.

Herleitung

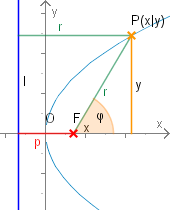
ParabelPolar.png
Es gilt cos⁡φ=x−p2r\cos\phi=\dfrac {x-\dfrac p 2} r also x−p2=rcos⁡φx-\dfrac p 2= r\cos\phi. Außerdem gilt: x+p2=rx+\dfrac p 2=r. Subtrahieren wir diese beiden Gleichungen, erhalten wir: p=r(1−cos⁡φ)p=r(1-\cos\phi). Führen wir jetzt eine Koordinatentransformation φ→π−φ\phi\rightarrow\pi-\phi durch, erhalten wir die Behauptung. □\qed
 
 

Man darf nicht das, was uns unwahrscheinlich und unnatürlich erscheint, mit dem verwechseln, was absolut unmöglich ist.

Carl Friedrich Gauß

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene