Kreis und Kreisgleichung

In der Elementargeometrie wurde ein Kreis als Menge aller Punkte mit einem festen Abstand zu einem vorgegebenen Punkt definiert.
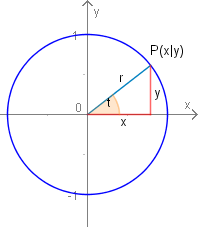
KreisPd.png
Betrachten wir den Kreis analytisch, so können wir unter Benutzung des Satzes des Pythagoras folgende Formel für eine Kreis um den Ursprung angeben.

Formel 15VR (Kreisgleichung in Normalform)

x2+y2=r2x^2+y^2=r^2
In Vektorschreibweise: ⟨p,p⟩=r2\spo p,p\spc=r^2
Für einen Kreis mit dem Mittelpunkt (x0∣y0)(x_0|y_0) ergibt sich:
(x−x0)2+(y−y0)2=r2(x-x_0)^2+(y-y_0)^2=r^2
Betrachtet man als Parameter tt den Winkel der Strecke OP‾\overline{OP} mit der xx-Achse, so ergibt sich:

Formel 15VS (Kreisgleichung in Parameterform)

x=r⋅cos⁡tx=r\cdot\cos t y=r⋅sin⁡ty=r\cdot\sin t
Für einen Kreis mit dem Mittelpunkt (x0∣y0)(x_0|y_0):
x=x0+r⋅cos⁡tx=x_0+r\cdot\cos t y=y0+r⋅sin⁡ty=y_0+r\cdot\sin t
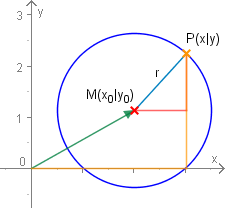
KreisPd1.png
Unter Benutzung von Satz 5220B kann man hieraus wieder Formel 15VR ableiten.
 
 

Das ist ein Mittel, das Paradies nicht zu verfehlen: auf der einen Seite einen Mathematiker, auf der anderen einen Jesuiten; mit dieser Begleitung muß man seinen Weg machen, oder man macht ihn niemals.

Friedrich der Große

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene