Zusammenfassung
Die Formel
gilt für Ellipse, Hyperbel und Parabel in Polarkoordinaten. Daher ist ein enger Zusammenhang zwischen den Kurven zu vermuten.
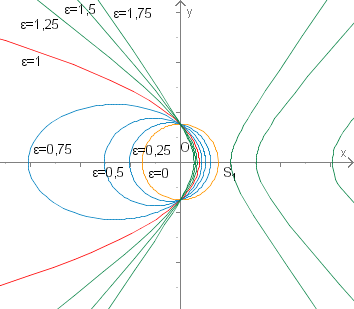
Die Grafik veranschaulicht den Übergang der Kurven ineinander bei wachsenden .
Alle Kurven zweiter Ordnung kann man auch als Kegelschnitte interpretieren. Dabei wird ein gerader Kreiskegel von einer Ebene geschnitten. Je nach Lage der Ebene entsteht eine Ellipse, Hyperbel oder Parabel.

An Archimedes wird man sich erinnern, wenn Aischylos vergessen ist - weil zwar die Sprachen sterben, nicht aber die mathematischen Ideen.
Godfrey Harold Hardy
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе