Kegelschnitte

Kegelschnitte.png
Schnitt eines Kegels mit einer Ebene
Ein Kegelschnitt (englisch conic section, cone-plane intersection) ist eine Kurve, die entsteht, wenn man die Oberfläche eines unendlichen Kegels bzw. Doppelkegels mit einer Ebene schneidet.

Klassifikation der Kegelschnitte

Es können folgende Figuren entstehen:
  • ein Punkt, wenn die Schnittebene durch die Spitze geht und der Winkel zwischen Achse und Ebene größer als der Öffnungswinkel ist
  • eine Gerade, wenn die Schnittebene durch die Spitze geht und der Winkel zwischen Achse und Ebene gleich dem Öffnungswinkel ist
  • zwei sich schneidende Geraden, wenn die Schnittebene durch die Spitze geht und der Winkel zwischen Achse und Ebene kleiner als der Öffnungswinkel ist
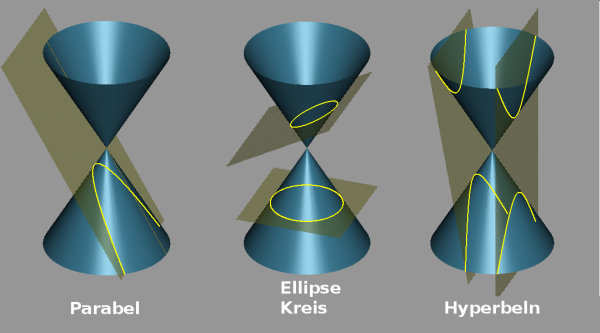
  • ein Kreis, wenn die Schnittebene senkrecht (orthogonal) auf der Kegelachse steht
  • eine Ellipse, wenn der Winkel zwischen Achse und Ebene größer als der Öffnungswinkel ist
  • eine Parabel, wenn der Winkel zwischen Achse und Ebene gleich dem Öffnungswinkel ist
  • eine Hyperbel, wenn der Winkel zwischen Achse und Ebene kleiner als der Öffnungswinkel ist
Kegelschnitt.png

Die allgemeine Kegelschnittgleichung

Im ebenen kartesischen Koordinatensystem ist der Graph einer quadratischen Gleichung (mit den Variablen xx und yy) immer ein Kegelschnitt. Umgekehrt können alle Kegelschnitte durch solche Gleichungen beschrieben werden. Die allgemeine Gleichung für Kegelschnitte lautet also
ax2+2bxy+cy2+2dx+2ey+f = 0,a x^2 + 2 b x y + c y^2 + 2 d x + 2 e y + f \, = \, 0,
wobei der Faktor 2 bei den Koeffizienten b, db,\, d und ee aus Gründen der Zweckmäßigkeit verwendet wird.
Der Typ des Kegelschnitts ergibt sich aus den im Folgenden definierten Determinanten Δ\Delta und δ\delta sowie der Summe SS:
Δ = ∣abdbcedef∣\Delta \, = \, \begin{vmatrix} a & b & d \\ b & c & e \\ d & e & f \end{vmatrix}; δ = ∣abbc∣=ac−b2\delta \, = \, \begin{vmatrix} a & b \\ b & c \end{vmatrix} = ac-b^2; S = a+cS \, = \, a + c
  • Für δ>0\delta > 0 und Δ⋅S<0\Delta \cdot S < 0 handelt es sich um eine Ellipse. Gilt zusätzlich a=ca = c und b=0b = 0, so ist diese Ellipse sogar ein Kreis.
  • Gelten die Bedingungen δ<0\delta < 0 und Δ≠0\Delta \ne 0, so ergibt sich eine Hyperbel, die im speziellen Fall a+c=0a + c = 0 gleichseitig (rechtwinklig) ist.
  • Unter den Voraussetzungen δ=0\delta = 0 und Δ≠0\Delta \ne 0 beschreibt die Gleichung eine Parabel.
  • Wenn Δ=0\Delta = 0 und δ=0\delta = 0 kommt ein paralleles Geradenpaar heraus.
  • Ist Δ=0\Delta = 0 und δ>0\delta > 0 kommt ein imaginäres Geradenpaar heraus.
  • Sollte Δ=0\Delta = 0 und δ<0\delta < 0 kommt als Lösung ein reelles Geradenpaar heraus.
Soweit es sich um eine Ellipse, Hyperbel oder Parabel handelt, bedeutet die Bedingung b=0b = 0, dass die Achsen parallel zu den Koordinatenachsen verlaufen. Im allgemeinen Fall lässt sich der Drehwinkel gegenüber der achsenparallelen Lage durch
tan⁡(2α) = 2ba−c\tan (2 \alpha) \, = \, \dfrac{2 b}{a - c}
berechnen.
Folgerungen aus der allgemeinen Kegelschnittsgleichung:
  • Ein Kegelschnitt ist durch fünf Punkte eindeutig festgelegt.
  • Zwei verschiedene Kegelschnitte schneiden einander höchstens in vier Punkten.
Besonders elegant wird die Kegelschnittgleichung unter Verwendung homogener Koordinaten: Alle Punkte X X , die auf dem Kegelschnitt mit der Matrix C C liegen, erfüllen die homogene Kegelschnitt-Gleichung:
XTCX=0 X^T C X = 0 , C=(abdbcedef)C = \begin{pmatrix} a & b & d \\ b & c & e \\ d & e & f \end{pmatrix}, X=(xyw)X = \begin{pmatrix} x \\ y \\ w \end{pmatrix}
Die Matrix C definiert hierbei den Kegelschnitt vollständig und wird daher oft selbst auch als Conic bezeichnet. Für alle X, die die obige Gleichung nicht erfüllen, gibt das Vorzeichen des Ergebnisses darüber Aufschluß, ob der Punkt innerhalb/außerhalb (bzw. auf welcher Seite) des Conics liegt. Wie viele andere Objekte der projektiven Geometrie auch, ändert eine Skalierung der Matrix nichts an den Objekteigenschaften, die Multiplikation mit einem negativen Wert ändert allerdings die Interpretation von innen und außen.
Die oben beschriebenen Kegelschnitte sind sogenannte Punkt-Conics, d.h. alle Punkte, die auf der Kurve liegen, erfüllen die Gleichung. Invertiert man nun die Matrix C, gelangt man zum Dualen Conic (oder Linien-Conic)
D = C−1 D \ = \ C^{-1}
Alle Geraden G (in homogener Darstellung), die Tangenten an den Punkt-Conic sind, erfüllen die Gleichung
GT D G=0 G^T \ D \ G = 0
Die Conic-Matrix ist eine implizite Form der Kurve oder der Menge von Tangenten. Man kann sehr leicht prüfen, ob ein Punkt X auf dem Kegelschnitt liegt oder nicht, aber die Form liefert keine Parametrisierung zum "Entlanglaufen". Das bedeutet, dass, gegeben die Matrix, es nicht direkt möglich ist, einen Punkt zu finden, der auf dem Objekt liegt, dafür muss man den Kegelschnitt in eine explizite Form überführen.

Anwendungen und Beispiele

Eine Anwendung finden die Kegelschnitte in der Astronomie, da die Bahnen der Himmelskörper genäherte Kegelschnitte sind.
Auch in der Optik werden sie verwendet - als Rotationsellipsoid für Autoscheinwerfer, als Paraboloid oder Hyperboloid für Spiegelteleskope usw.
 
 

Das entscheidende Kriterium ist Schönheit; für häßliche Mathematik ist auf dieser Welt kein beständiger Platz.

Godfrey Harold Hardy

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Kegelschnitt aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene