Hyperboloid

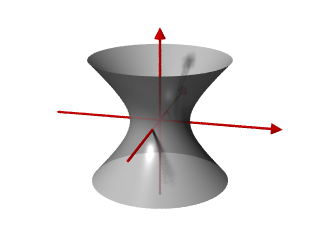
Hyperboloid1.pov.png
einschaliges Hyperboloid
Ein Hyperboloid ist eine Fläche 2. Ordnung, die durch Ebenen in Hyperbeln, Ellipsen, Parabeln geschnitten werden kann.
Es wird zwischen ein- und zweischaligen Hyperboloiden unterschieden. Das einschalige Hyperboloid gleicht einem Kühlturm, auf der Oberfläche liegen zwei Scharen von Geraden. Das zweischalige Hyperboloid besteht aus zwei nicht miteinander verbundenen Teilflächen, es enthält keine reellen Geraden.
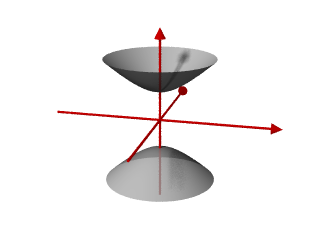
Hyperboloid2.pov.png
zweischaliges Hyperboloid
Die Formel für ein Hyperboloid ist:
  • einschalig: x2a2+y2b2−z2c2=1\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2} = 1
  • zweischalig: x2a2+y2b2−z2c2=−1\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2} = -1
Der Grenzfall zwischen ein- und zweischaligem Hyperboloiden, wenn sich die beiden Schalen in einem Punkt berühren, ist der Doppelkegel:
  • Doppelkegel: x2a2+y2b2−z2c2=0\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} - \dfrac{z^2}{c^2} = 0
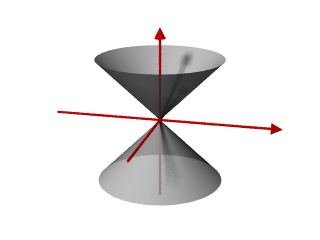
Doppelkegel.pov.png
Doppelkegel
Ein Hyperboloid mit a=ba=b wird auch als Rotationshyperboloid bezeichnet.
Siehe auch: Paraboloid, Ellipsoid, Zylinder
 
 

Ich stimme mit der Mathematik nicht überein. Ich meine, daß die Summe von Nullen eine gefährliche Zahl ist.

Stanislaw Jerzy Lec

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Hyperboloid aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Raum