Spatprodukt

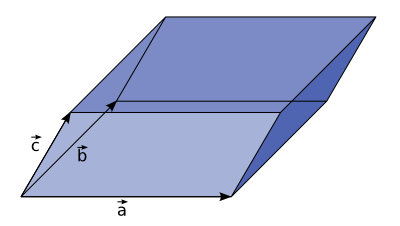
Parallelepiped2.png
Spat, der von drei Vektoren aufgespannt wird
Das Spatprodukt ist das Skalarprodukt aus dem Kreuzprodukt zweier Vektoren und einem dritten Vektor. Es ergibt das orientierte Volumen des durch die drei Vektoren aufgespannten Spats (Parallelepipeds). Es wird auch gemischtes Produkt genannt und ist identisch mit der aus diesen Vektoren gebildeten Determinante, also:
Va,b,c=(a×b)⋅cV_{\vec{a},\vec{b},\vec{c}} = (\vec{a} \times \vec{b}) \cdot \vec{c} =(b×c)⋅a= (\vec{b} \times \vec{c}) \cdot \vec{a} =(c×a)⋅b= (\vec{c} \times \vec{a}) \cdot \vec{b} =det⁡(a1a2a3b1b2b3c1c2c3) = \det\begin{pmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_ 3 \\ c_1 & c_2 & c_3 \end{pmatrix} =det⁡(a1b1c1a2b2c2a3b3c3)= \det\begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_ 2 \\ a_3 & b_3 & c_3\end{pmatrix}

Eigenschaften und Notation

Das Spatprodukt ist nicht kommutativ. Wie schon oben verwendet, gilt allgemein
(a×b)⋅c=a⋅(b×c)(\vec{a} \times \vec{b}) \cdot \vec{c} = \vec{a} \cdot (\vec{b} \times \vec{c}).
Man kann also bei entsprechend angepasster Klammerung (die anders unsinnig wäre) die beiden Rechenzeichen "vertauschen". Der Beweis kann durch einfaches Ausrechnen erbracht werden. Wegen dieser Möglichkeit der zyklischen Vertauschung findet man auch Notationen des Spatprodukts, bei denen die Rechenzeichen einfach weggelassen sind:
(a×b)⋅c=(a,b,c)=[a,b,c]=⟨a,b,c⟩(\vec{a} \times \vec{b}) \cdot \vec{c} = \left( \vec{a}, \vec{b}, \vec{c} \right) = \left[ \vec{a}, \vec{b}, \vec{c} \right] = \langle \vec{a}, \vec{b}, \vec{c} \rangle.
Im Gegensatz zur zyklischen Vertauschung tritt bei der antizyklischen Vertauschung ein Vorzeichenwechsel auf:
(a,b,c)=−(b,a,c)\left( \vec{a}, \vec{b}, \vec{c} \right) = - \left( \vec{b}, \vec{a}, \vec{c} \right)
Weiter gilt wegen a×a=0\vec{a}\times\vec{a}=\vec{0}:
(a,a,b)=0\left( \vec{a}, \vec{a}, \vec{b} \right) = 0.
Auch die Multiplikation mit einem Skalar α∈R\alpha \in \mathbb{R} ist assoziativ:
(α⋅a,b,c)=α⋅(a,b,c)\left( \alpha \cdot \vec{a}, \vec{b}, \vec{c} \right) = \alpha \cdot \left( \vec{a}, \vec{b}, \vec{c} \right).
Und es gilt ein Distributivgesetz:
(a,b,c+d)=(a,b,c)+(a,b,d) \left( \vec{a}, \vec{b}, \vec{c} + \vec{d} \right) = \left( \vec{a}, \vec{b}, \vec{c} \right) + \left( \vec{a}, \vec{b}, \vec{d} \right)\, .

Geometrische Herleitung

Das Volumen eines Spats errechnet sich aus dem Produkt seiner Grundfläche und seiner Höhe.
V=Ag⋅hV = A_g \cdot h
Bekanntlich ist das Kreuzprodukt a×b\vec{a}\times\vec{b} genau der Normalenvektor auf der durch aa und bb aufgespannten Grundfläche, der mit aa und bb ein rechtshändiges Koordinatensystem bildet und dessen Betrag gleich dem Flächeninhalt dieser Fläche ist, also Ag=∣a×b∣A_g=\left| \vec{a}\times\vec{b} \right|.
Die Höhe des Spats ist die Projektion des Vektors cc auf die Richtung dieses Normalenvektors (dessen Einheitsvektor). Wenn diese den Winkel α\alpha einschließen, gilt nach der Definition des Skalarprodukts
h=∣c∣cos⁡α=e^(a×b)⋅c h = \left| \vec{c} \right| \cos \alpha = \hat e_{\left(\vec{a} \times \vec{b}\right)} \cdot \vec{c}
Es folgt
V=Ag⋅h=∣a×b∣(e^(a×b)⋅c)=(a×b)⋅c V = A_g \cdot h = \left| \vec{a}\times\vec{b} \right| ( \hat e_{\left(\vec{a} \times \vec{b}\right)} \cdot \vec{c}) = \left(\vec{a} \times \vec{b}\right) \cdot \vec{c}
Das Volumen ist Null für α\alpha gleich 90°, wenn also die Vektoren in einer Ebene liegen. Sie heißen dann komplanar und linear abhängig.
Das (orientierte) Volumen ist negativ, falls α\alpha größer ist als 90°. Dann zeigen Vektorprodukt und projizierte Höhe in entgegengesetzte Richtungen, weil die Vektoren ein Linkssystem bilden.

Algebraische Herleitung

Das Spatprodukt kann auch mit dem Levi-Civita-Symbol hergeleitet werden. Dafür wird zuerst das Skalarprodukt durch eine Summe dargestellt:
(a×b)⋅c=∑i=13(a×b)i⋅ci  (\vec{a} \times \vec{b}) \cdot \vec c = \sum\limits_{i=1}^3 (\vec{a} \times \vec{b})_i \cdot c_i\,
Das Kreuzprodukt wird nun mit dem Levi-Civita-Symbol durch eine Summenschreibweise dargestellt:
∑i=13(a×b)i⋅ci=∑i=13∑j=13∑k=13εijkajbkci  \sum\limits_{i=1}^3 (\vec{a} \times \vec{b})_i \cdot c_i = \sum\limits_{i=1}^3 \sum\limits_{j=1}^3 \sum\limits_{k=1}^3 \varepsilon_{ijk} a_j b_k c_i\,
Der total antisymmetrische Epsilontensor εijk\varepsilon_{ijk} ist gleich εkij\varepsilon_{kij} bzw. gleich εjki\varepsilon_{jki}. Damit lässt sich das Spatprodukt wie folgt ausdrücken:
∑i=13∑j=13∑k=13εijkajbkci=∑i=13∑j=13∑k=13εkijajbkci=∑i=13∑j=13∑k=13εjkiajbkci  \sum\limits_{i=1}^3 \sum\limits_{j=1}^3 \sum\limits_{k=1}^3 \varepsilon_{ijk} a_j b_k c_i = \sum\limits_{i=1}^3 \sum\limits_{j=1}^3 \sum\limits_{k=1}^3 \varepsilon_{kij} a_j b_k c_i = \sum\limits_{i=1}^3 \sum\limits_{j=1}^3 \sum\limits_{k=1}^3 \varepsilon_{jki} a_j b_k c_i\,
Die Summenzeichen können vertauscht werden. Außerdem kann man nun geschickt Klammern setzen:
∑i=13(∑j=13∑k=13εijkajbk)ci=∑k=13(∑i=13∑j=13εkijciaj)bk=∑j=13(∑k=13∑i=13εjkibkci)aj  \sum\limits_{i=1}^3 (\sum\limits_{j=1}^3 \sum\limits_{k=1}^3 \varepsilon_{ijk} a_j b_k) c_i = \sum\limits_{k=1}^3 (\sum\limits_{i=1}^3 \sum\limits_{j=1}^3 \varepsilon_{kij} c_i a_j) b_k = \sum\limits_{j=1}^3 (\sum\limits_{k=1}^3 \sum\limits_{i=1}^3 \varepsilon_{jki} b_k c_i) a_j\,
Schreibt man die Kreuzprodukte nun wieder ohne Levi-Civita-Symbol, so ergibt sich die gewünschte Identität:
(a×b)⋅c=(c×a)⋅b=(b×c)⋅a (\vec{a} \times \vec{b}) \cdot \vec{c} = (\vec{c} \times \vec{a}) \cdot \vec{b} = (\vec{b} \times \vec{c}) \cdot \vec{a}\,

Literatur

  • Wolfgang Gawronski: Grundlagen der Linearen Algebra. Aula-Verlag, Wiesbaden 1996, ISBN 3-89104-566-2
 
 

Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.

Michael Stifel

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Spatprodukt aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Analytische Geometrie