Winkel

Winkel.png
Abb. 1: Zur Definition des Winkels.
Zwei vom Punkt AA ausgehende Strecken AB‾\overline {AB} und AC‾\overline {AC} bestimmen den Winkel ∠BAC\angle BAC. Durch diesen Winkel wird eine Drehung festgelegt, die die durch BB gehende Halbgerade in die durch CC verlaufende überführt. Der Punkt AA heißt Scheitelpunkt des Winkels. Die Strahlen ausgehende vom Scheitel AA durch die Punkte BB und CC heißen Schenkel.
Bei der Definition von Winkeln spielt die Orientierung eine entscheidende Rolle. Im Allgemeinen wird die Drehung als gegen den Uhrzeigersinn (mathematisch positiv) betrachtet.
Winkel werden mit kleinen griechischen Buchstaben wie α\alpha, β\beta, γ\gamma, ... bezeichnet.

Winkelmessung

Zur Messung der Winkel benutzt man die Einheit Grad (Symbol: °). Dabei entspricht der Vollwinkel 360°. Diese Maß heißt Gradmaß. Eine andere Möglichkeit ist das Bogenmaß. Dabei entspricht dem Vollwinkel die Größe 2π2\pi. (Für Details siehe: Winkelmaße.)

Einteilung der Winkel

Nach ihrer Größe können die Winkel wie folgt eingeteilt werden.
Name Beispiel Größe
spitzer Winkel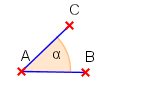
WSpitz.png
 0<α<90°0< \alpha< 90°
rechter Winkel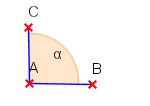
WRecht.png
 α=90°\alpha=90°
stumpfer Winkel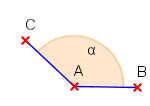
WStumpf.png
 90°<α<180°90°< \alpha< 180°
gestreckter Winkel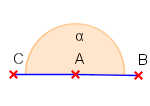
WGestr.png
 α=180°\alpha=180°
überstumpfer Winkel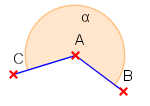
WUStrumpf.png
 180°<α<360°180°< \alpha< 360°
Vollwinkel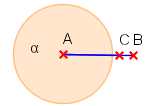
WVoll.png
 α=360°\alpha=360°

Winkel an einander sich schneidenden Geraden

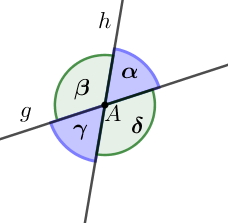
WinkelGeraden.png
Abb. 2: Scheitelwinkelpaare an geschnittenen Geraden.
Schneiden sich die Geraden g\displaystyle{{g}} und h\displaystyle{{h}} im Punkt A\displaystyle{{A}}, so entstehen vier Winkel, die in Abb. 2 mit α\displaystyle{\alpha}, β\displaystyle{\beta}, γ\displaystyle{\gamma} und δ\displaystyle{\delta} bezeichnet sind. Die Winkelpaare α\displaystyle{\alpha}, γ\displaystyle{\gamma} und β\displaystyle{\beta}, δ\displaystyle{\delta} heißen Scheitelwinkel. Es gilt
α+β=β+γ=γ+δ=δ+α=180°\displaystyle{\alpha+\beta=\beta+\gamma=\gamma+\delta=\delta+\alpha={180}°},
da diese Winkel gestreckte Winkel sind.
Nun ist dann α+β−(β+γ)=α−γ=0°\displaystyle{\alpha+\beta-{\left(\beta+\gamma\right)}=\alpha-\gamma={0}°}, also α=γ\displaystyle{\alpha=\gamma}. Ebenso kann man β=δ\displaystyle{\beta=\delta} herleiten. Es zeigt sich damit:
Daher sind diese in Abb. 2 mit der gleichen Farbe gekennzeichnet worden.
 
 

Im großen Garten der Geometrie kann sich jeder nach seinem Geschmack einen Strauß pflücken.

David Hilbert

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie