Strahlensätze

Der Strahlensatz (man spricht auch vom ersten, zweiten und dritten Strahlensatz) oder Vierstreckensatz befasst sich mit Streckenverhältnissen und ermöglicht es bei vielen geometrischen Überlegungen, unbekannte Streckenlängen auszurechnen.

Formulierung der Strahlensätze

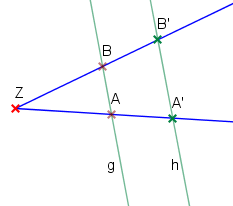
ssatz1.png
Wenn zwei durch einen Punkt ZZ (Scheitel) verlaufende Geraden von zwei parallelen Geraden g∣∣hg||h geschnitten werden, die nicht durch den Scheitel gehen, dann gilt:
 
 

1. Strahlensatz

Je zwei Abschnitte auf dem einen Strahl verhalten sich wie die entsprechenden Abschnitte auf dem anderen Strahl.
ZA‾ZA′‾=ZB‾ZB′‾\dfrac {\overline {ZA}} {\overline {ZA'}} =\dfrac{ \overline {ZB}} {\overline {ZB'} }(1)

2. Strahlensatz

Die ausgeschnittenen Strecken auf den Parallelen verhalten sich wie die vom Scheitel aus gemessenen Strecken auf den Strahlen.
AB‾A′B′‾=ZA‾ZA′‾=ZB‾ZB′‾\dfrac {\overline {AB}} {\overline {A'B'}} =\dfrac {\overline {ZA} }{\overline {ZA'}} =\dfrac {\overline {ZB}}{ \overline {ZB'}} (2)
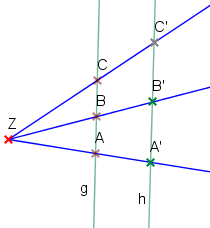
ssatz3.png

3. Strahlensatz

Dieser Strahlensatz setzt im Gegensatz zu den ersten beiden Strahlensätzen mindestens drei Strahlen voraus und kann leicht aus den vorhergehenden hergeleitet werden.
Je zwei Abschnitte auf den Parallelen, die einander entsprechen, stehen in gleichem Verhältnis zueinander.
AB‾BC‾=A′B′‾B′C′‾\dfrac{ \overline {AB}} {\overline {BC}} =\dfrac {\overline {A'B'}}{ \overline {B'C'}} (3)
Der erste Strahlensatz bezieht sich also auf die Verhältnisse von Strahlenabschnitten, der zweite auf die Verhältnisse von Strahlen- und Parallelenabschnitten und der dritte auf die Verhältnisse von Parallelenabschnitten.

Umkehrung

Für alle Strahlensätze gilt auch die Umkehrung, mittels der man aus der Gültigkeit einer der Verhältnisgleichungen (1) (2) oder (3) auf die Parallelität der Geraden gg und hh schließen kann.

Alle Pädagogen sind sich darin einig: man muß vor allem tüchtig Mathematik treiben, weil ihre Kenntnis fürs Leben größten direkten Nutzen gewährt.

Felix Klein

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie