Zentrische Streckung

Unter einer zentrischen Streckung versteht man in der Geometrie eine Abbildung, die alle Strecken in einem bestimmten, gegebenen Verhältnis vergrößert oder verkleinert, wobei die Bildstrecken jeweils zu den ursprünglichen Strecken parallel sind. Zentrische Streckungen sind spezielle Ähnlichkeitsabbildungen.
 
 

Definition

ZentrStreckPos.png
Gegeben seien ein Punkt ZZ der Zeichenebene oder des Raumes und eine reelle Zahl m≠0m \ne 0. Die zentrische Streckung mit Zentrum ZZ und Streckungsfaktor (Abbildungsfaktor) mm ist diejenige Abbildung der Zeichenebene beziehungsweise des Raumes in sich, bei der der Bildpunkt P′P' eines Punktes PP folgende Eigenschaften besitzt:
  • Z, PZ,\, P und P′P' liegen auf einer Geraden.
  • Für m>0m>0 liegen PP und P′P' auf derselben Seite von ZZ, für m<0m<0 auf verschiedenen Seiten.
  • Die Streckenlänge ZP′‾\overline{ZP'} ist gleich dem ∣m∣|m|-fachen der Streckenlänge ZP‾\overline{ZP}.
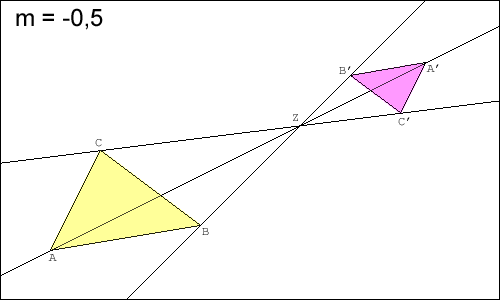
ZentrStreckNeg.png
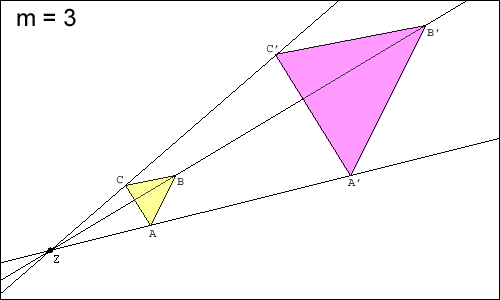
Die beiden Skizzen zeigen die Anwendung zweier zentrischer Streckungen (mit m=3m = 3 und m=−0,5m = -0{,}5) auf jeweils ein Dreieck ABC.

Eigenschaften

  • Zentrische Streckungen sind geraden- und winkeltreu, aber im Allgemeinen nicht längentreu.
  • Die Bildstrecke einer beliebigen Strecke hat die ∣m∣|m|-fache Länge.
  • Eine beliebige geometrische Figur wird auf eine Figur mit dem m2m^2-fachen Flächeninhalt abgebildet.
  • Ein beliebiger Körper wird auf einen Körper mit dem ∣m∣3|m|^3-fachen Volumen abgebildet.
  • Die zentrischen Streckungen mit einem bestimmten Zentrum bilden algebraisch gesehen eine Gruppe.

Spezialfälle

Für m=1m = 1 ergibt sich die identische Abbildung (Identität), für m=−1m = -1 eine Punktspiegelung. Der Fall m=0m = 0 ist nicht erlaubt, da sonst alle Punkte denselben Bildpunkt hätten, nämlich das Zentrum.

Die ganzen Zahlen hat der liebe Gott geschaffen, alles andere ist Menschenwerk.

Leopold Kronecker

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Zentrische Streckung aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie