Weitere Definitionen der ebenen Geometrie

Senkrechte Geraden

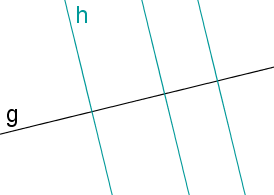
SeGerade.png
Zwei Geraden gg und hh stehen senkrecht aufeinander (sind orthogonal zueinander) falls der Winkel zwischen ihnen 90°90° beträgt. Man schreibt dann g⊥hg\perp h. Zu gg gibt es unendlich viele senkrechte Geraden; jeweils zwei von ihnen sind jedoch stets parallel zueinander.
MiPunkt.png

Mittelpunkt und Mittelsenkrechte einer Strecke

Sei AB‾\ovl{AB} eine Strecke, dann heißt ein auf dieser Strecke liegender Punkt MM Mittelpunkt, falls seine Entfernung zum Punkt AA genauso groß ist, wie die zum Punkt BB. Der Mittelpunkt ist eindeutig bestimmt.
 
 

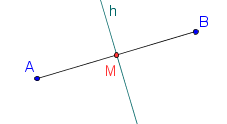
MiSenk.png
Eine durch den Mittelpunkt MM gehende senkrechte Gerade hh heißt Mittelsenkrechte zu AB‾\ovl{AB}. Die Mittelsenkrechte durch MM ist eindeutig bestimmt.

Winkelhalbierende

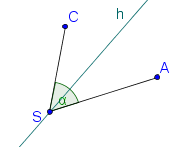
WiHalb.png
Die Winkelhalbierende ist die Menge aller Punkte, die von den beiden Schenkeln des Winkels den gleichen Abstand hat. Dabei handelt es sich um eine Gerade (hh in der nebenstehende [!Abbildung]). Die Winkelhalbierende ist eindeutig bestimmt.
Bei einem gestreckten Winkel fällt die Winkelhalbierende mit der Mittelsenkrechten durch den Scheitelpunkt zusammen.

Jede mathematische Formel in einem Buch halbiert die Verkaufszahl dieses Buches.

Stephen Hawking

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie