Polygone

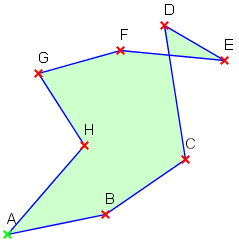
Polygon.png
Nicht konvexes, überschlagenes Polygon
Ein Polygon oder auch Vieleck bezeichnet eine von Strecken begrenzten ebene Figur. Diese Strecken heißen Seiten und ihre gemeinsamen Punkte Ecken des Polygons. Typische Vertreter sind Dreiecke, Vierecke und Sechsecke, wohingegen Kreise keine Polygone sind.

Definition

Seien für n>=3n>=3 P1,P2,…,Pn P_1, P_2, \ldots , P_n paarweise verschiedene Punkte der Ebene. Dann heißt die von den nn Strecken P1P2‾\nohtml \ovl{P_1P_2}, P2P3‾\nohtml \ovl{P_2P_3}, ... , PnP1‾\nohtml \ovl{P_nP_1} gebildetete geschlossene geometrische Figur ein Polygon. Nach der Anzahl der Ecken spricht man auch vom nn-Eck.
Die Punkte PiP_i heißen die Ecken des Polygons und die Strecken PiPi+1‾(i=1,…,n−1)\overline {P_i P_{i+1}} \braceNT{i=1, \ldots, n-1 } und PnP1‾\overlineI { P_n P_1 } seine Seiten oder auch Kanten
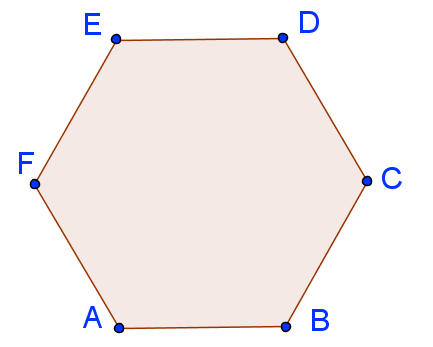
6e.png
Reguläres Sechseck
Schneiden oder berühren sich Kanten, so heißt dass Polygon überschlagen. Des weiteren wollen wir voraussetzen, dass drei aufeinanderfolgende Eckpunkte nicht kollinear sind, das Polygon also keine 180° großen Innenwinkel besitzt.
Verbindungsstrecken, die keine Kanten sind heißen Diagonalen.
 
 

Satz 5515L (Anzahl der Diagonalen im Polygon)

In einem Polygon mit nn Ecken gibt es
n(n−3)2\dfrac {n(n-3)} 2
Diagonalen.

Beweis

Es gibt
n(n−1)2\dfrac {n(n-1)} 2(1)
Möglichkeiten nn Punkte untereinander zu verbinden. Ein nn-Eck hat genau nn Seiten. Ziehen wir diese von (1) ab, erhalten wir mit
n(n−1)2−n=n2−n−2n2=n(n−3)2\dfrac {n(n-1)} 2-n=\dfrac {n^2-n -2n} 2= \dfrac {n(n-3)} 2
die Behauptung. □\qed

Satz C7PF (Innenwinkel in konvexen Polygonen)

In einem nicht überschlagenen, konvexen nn-Eck ist die Summe der Innenwinkel
α1+⋯+αn=(n−2)⋅180∘ \alpha_1+\dots +\alpha_n = (n - 2) \cdot 180^\circ.
Sind darüber hinaus alle Innenwinkel gleich groß, so haben diese den Wert
α=(n−2)n⋅180∘ \alpha = \dfrac{(n - 2)}{n} \cdot 180^\circ.

Beweisidee

Man führt den Beweis mittels vollständiger Induktion über die Eckenanzahl. Für n=3n=3 greift man auf Satz 5515C zurück. Im Induktionsschritt zerlegt man das n+1n+1-Eck durch eine Diagonale z.B. zwischen Pn−1P_{n-1} und P1P_1 in ein nn-Eck und ein Dreieck. Diese Diagonale liegt wegen der Konvexität innerhalb des Polygons und wir zeigen die Induktionsbehauptung durch Aufsummieren der Innenwinkel des nn-Ecks und der abgespalteten Dreiecks. □\qed

Miß alles, was sich messen läßt, und mach alles meßbar, was sich nicht messen läßt.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Elementargeometrie