Siebeneck

Heptagon.png
Regelmäßiges Siebeneck
Ein Siebeneck ist ein 'Vieleck (Polygon) mit sieben Punkten. Sofern nichts anderes gesagt wird, ist von einem ebenen, regelmäßigen Siebeneck die Rede (siehe Bild), dessen sieben Seiten gleich lang sind und dessen sieben Eckpunkte auf einem gemeinsamen Umkreis liegen.

Mathematische Zusammenhänge

Formel für Winkelberechnungen

Die Summe der Innenwinkel des Siebenecks beträgt stets 900° und ergibt sich aus einer allgemeinen Formel für Polygone, in der für die Variable n die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall: n = 7):
∑α=(n−2)⋅180∘=5⋅180∘=900∘ \sum\limits {\alpha =}(n - 2) \cdot 180^\circ = 5 \cdot 180^\circ = 900^\circ
Der Winkel, den zwei benachbarte Seitenkanten im ebenen, regelmäßigen Siebeneck miteinander einschließen, beträgt (wiederum nach einer allgemeinen Formel für regelmäßige Polygone):
α=(n−2)n⋅180∘=57⋅180∘≈128,57∘ \alpha =\dfrac{(n - 2)}{n} \cdot 180^\circ = \dfrac{5}{7} \cdot 180^\circ \approx 128,57^\circ
 
 

Formel für die Fläche A

A=74⋅s2⋅tan⁡450∘7≈3,63391⋅s2 A = \dfrac{7}{4} \cdot s^2 \cdot \tan{\dfrac{450^\circ}{7}} \approx 3,63391 \cdot s^2
oder mit dem Umkreisradius:
A=72⋅ru2⋅sin⁡360∘7≈2,73641⋅ru2 A = \dfrac{7}{2} \cdot r_u^2 \cdot \sin{\dfrac{360^\circ}{7}} \approx 2,73641 \cdot r_u^2

Formel für die Seitenlänge s

s=2⋅ru⋅sin⁡180∘7≈ru⋅0,867767478235s=2 \cdot r_u \cdot \sin{\dfrac{180^\circ}{7}} \approx r_u \cdot 0,867767478235

Näherungskonstruktionen

Ein regelmäßiges Siebeneck kann nicht mit Zirkel und Lineal exakt konstruiert, sondern nur berechnet werden.
Nach einem Beweis von Carl Friedrich Gauß sind, wenn n eine Primzahl ist, die und nur die n-Ecke konstruierbar, bei denen es natürliche Zahlen k gibt, so dass n eine Primzahl der Gestalt n=22k+1n=2^{2k}+1 ist. Das sind n = 3, 5, 17, ... für k = 0, 1, 2, ... Darunter ist also nicht n = 7. Deshalb kann eine Konstruktion für das regelmäßige Siebeneck nicht existieren.
Es gibt jedoch für die Praxis einige ausreichend genaue Näherungskonstruktionen.
Es geht darum, eine Strecke zu erhalten, welche möglichst genau das 0,86776747823-fache eines gegebenen Radius ist.
Eine sehr einfache Näherungskonstruktion ist in folgender Zeichnung dargestellt:
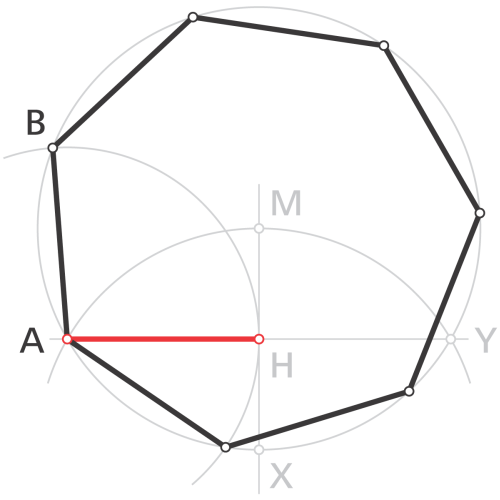
Siebeneck_Konstruktion1.png
  1. Vom Mittelpunkt des Umkreises zeichnet man eine Gerade, die den Umkreis im Punkt X schneidet.
  2. Dann zeichnet man einen Kreis um X, der durch M verläuft und den Umkreis in den Punkten A und Y schneidet.
  3. Die Gerade AY schneidet die Strecke MX‾\overline {MX} im Halbierungspunkt H.
  4. Die rote Strecke AH‾\overline {AH} ist eine gute Näherung für die Seitenlänge des Siebenecks.
  5. Die Eckpunkte B bis G erhält man durch Abschlagen der Seitenlänge am Umkreis.
Aus dem rechtwinkligen Dreieck AHM errechnet sich:
AH‾=MA‾2−MH‾2 \overline{AH} = \sqrt{ \overline{MA}^2 - \overline{MH}^2 \, }
Mit
MA‾=r\overline{MA} = r ; MH‾=12r\overline{MH} = \dfrac{1}{2}r und AH‾:=s\overline{AH} := s
s=r2−(12r)2  s = \sqrt{ r^2 - \braceNT{\dfrac{1}{2} r }^2 \, }
s=r⋅1−(12)2  s = r \cdot \sqrt{ 1 - \braceNT{\dfrac{1}{2} }^2 \, }
s≈r⋅0,8660254 s \approx r \cdot 0,8660254
Bei dieser Konstruktion beträgt der Fehler
f=0,8660254−0,86776750,8677675≈−0,002 f = \dfrac{0,8660254 - 0,8677675}{0,8677675} \approx - 0,002
Die mit dieser Konstruktion gewonnene Seitenlänge ist etwas zu kurz und beträgt 99,8 Prozent des wahren Wertes. Oder anders formuliert: Ab einem Umkreisradius von ca. 57,4 cm beträgt der Fehler in der Seitenlänge mehr als einen Millimeter.
Eine etwas aufwändigere aber verblüffend genaue Näherungskonstruktion ist in folgender Zeichnung dargestellt:
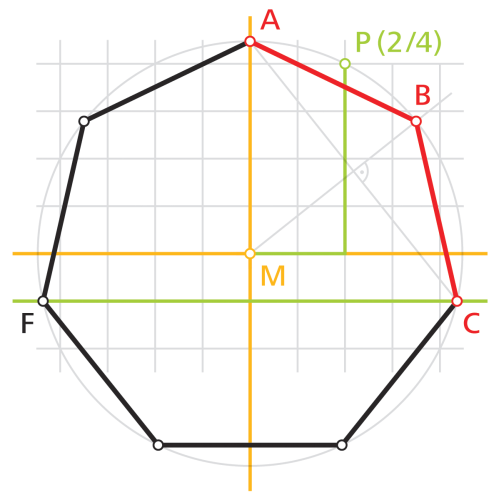
Siebeneck_Konstruktion2.png
  1. In einem rechtwinkeligen Koordinatensystem zeichnet man einen Kreis, der seinen Mittelpunkt im Ursprung (0/0) hat und genau durch den Punkt P mit den Koordinaten (2/4) verläuft.
  2. Der Schnittpunkt der positiven y-Achse mit der Kreislinie wird als Eckpunkt A des regelmäßigen Siebenecks festgelegt.
  3. Die Gerade y = -1 (horizontale grüne Linie) schneidet die Kreislinie in unmittelbarer Nähe der Eckpunkte C und F.
  4. Wenn man die Streckensymmetrale der Strecke AC mit dem Kreis schneidet, erhält man eine Näherung für den Eckpunkt B.
  5. Die rote Strecke Unknown meta: Overline|AB bzw. Unknown meta: Overline|BC ist eine sehr gute Näherung für die Seitenlänge des regelmäßigen Siebenecks.
  6. Die Eckpunkte D, E und G erhält man durch Spiegelung bzw. Abschlagen der Seitenlänge am Umkreis.
Bezeichnet man den Umkreisradius mit r, den Abstand der FC‾\overline{FC} von M mit h, und substituiert q=hr q = \dfrac{h}{r} so ergibt sich bei dieser Konstruktion:
AB‾=r⋅2−2⋅1−q\overline{AB} = r \cdot \sqrt{2 - \sqrt{2} \cdot \sqrt{1- q }}
und mit den Werten
r=20;h=1;q=120 r = \sqrt{20} ; h = 1 ; q = \dfrac{1}{\sqrt{20}}
ergibt sich:
AB‾=r⋅2−2⋅1−120\overline{AB} = r \cdot \sqrt{2 - \sqrt{2} \cdot \sqrt{1- \dfrac{1}{\sqrt{20}} }}
AB‾≈r⋅0,868269253\overline{AB} \approx r \cdot 0,868269253
Die mit dieser Konstruktion gewonnene Seitenlänge ist also etwas zu lang und der Fehler beträgt ca. 0,00057821133 , also 0,0578 Prozent. Oder anders formuliert: Bei einem Umkreisradius von ca. 199,3 cm beträgt der Fehler in der Seitenlänge einen Millimeter.

Seit der Zeit der Griechen bedeutet "Mathematik" zu sagen, "Beweis" zu sagen.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Siebeneck aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie