Spiegelungen
Bestimmte Arten von Kongruenzabbildungen der Zeichenebene in sich werden als Spiegelungen bezeichnet.
Punktspiegelung
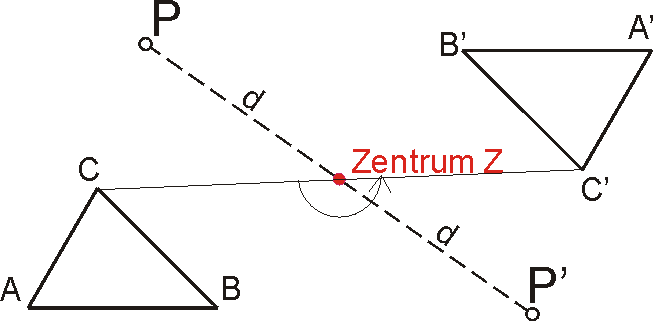
Halbieren der Verbindungsstrecke; Halbdrehung
Es handelt sich um eine Abbildung, die durch einen Punkt Z (Spiegelpunkt, Zentrum) gegeben ist. Die Spiegelung am Punkt Z ordnet jedem Punkt P der Zeichenebene oder jedem Punkt des Raumes einen Bildpunkt P' zu, der dadurch bestimmt ist, dass die Verbindungsstrecke [PP'] vom Punkt Z halbiert wird.
Zuweilen wird die Punktspiegelung auch als Inversion bezeichnet; man beachte jedoch, dass die Bezeichnung Inversion häufig für eine andere Abbildung, die Spiegelung an einem Kreis, benutzt wird.
Eine Punktspiegelung hat genau einen Fixpunkt (das heißt einen Punkt, den die Abbildung unverändert lässt), nämlich das Zentrum Z. Fixgeraden (also die Geraden, die die Abbildung in sich selbst überführt) sind genau die Geraden durch Z. Eine beliebige Gerade g wird auf eine zu g parallele Gerade (Bildgerade) g' abgebildet.
In der Ebene ist die Punktspiegelung am Zentrum Z gleichbedeutend mit einer Drehung um 180° bezüglich eines Drehzentrums Z.
Punktspiegelungen sind geraden-, längen- und winkeltreu, also Kongruenzabbildungen. Jede Punktspiegelung lässt sich ersetzen durch zwei hintereinander ausgeführte Achsenspiegelungen, wobei die Achsen dieser Spiegelungen durch das Zentrum Z gehen und zueinander senkrecht sind.
Achsenspiegelung
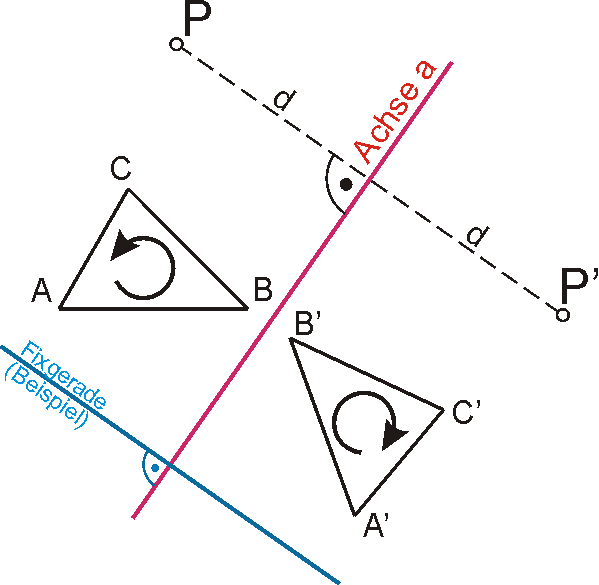
Rechtwinkliges Halbieren, Änderung des Umlaufsinns, Fixgeraden (rot und blau)
Die Achsenspiegelung (auch Geradenspiegelung) ist durch eine Gerade a (Spiegelachse oder kurz Achse) gegeben. Sie ordnet jedem Punkt P einen Bildpunkt P' zu, der dadurch bestimmt ist, dass die Verbindungsstrecke [PP'] von der Achse a rechtwinklig halbiert wird.
Die Fixpunkte einer Achsenspiegelung sind genau die Punkte von a. Man spricht daher auch von der Fixpunktgeraden a. Die Fixgeraden der Achsenspiegelung sind genau die Achse a selbst sowie alle Lotgeraden zur Achse. Im räumlichen Fall gibt es auch Fixebenen, nämlich die zur Achse a orthogonalen Ebenen.
Auch die Achsenspiegelung ist eine Kongruenzabbildung. Wenn zwei kongruente Objekte vorliegen, können diese in jedem Fall durch Komposition (Verkettung, Hintereinanderausführung) von höchstens drei Achsenspiegelungen ineinander übergeführt werden. Die Achsenspiegelung kann deshalb als ein Grundbegriff der metrischen Geometrie verwendet werden.
In der Ebene ist zu beachten, dass durch eine Achsenspiegelung der Umlaufsinn eines Dreiecks geändert wird. Sie ist also keine eigentliche "Bewegung", das heißt, sie kann nicht durch eine physikalische Bewegung verwirklicht werden, ohne dass das Objekt die Ebene verlässt.
Im dreidimensionalen Raum entspricht die Achsenspiegelung einer Drehung um 180° um die Spiegelachse. Ein Objekt, das zusammen mit der Spiegelachse in einer Ebene liegt, wird dabei in die gleiche Ebene "umgeklappt"; dies ist die Bewegung, die bei der Beschränkung auf eine Ebene nicht möglich war.
Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.
Bertrand Russell
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Spiegelung (Geometrie)
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе