Gleitspiegelungen
Unter einer Gleitspiegelung oder Schubspiegelung versteht man die Hintereinanderausführung einer Parallelverschiebung und einer Geradenspiegelung, bei der die Verschiebung parallel zur Geraden geschieht.
Als Kongruenzabbildungen erhalten Gleitspiegelungen Längen, d.h. eine "gleitgespiegelte" Strecke ist genauso lang wie das Original. Gleitspiegelungen sind daher Isometrien. Allerdings erhalten Gleitspiegelungen nicht die Orientierung einer Figur.
Gleitspiegelungen spielen besonders in der diskreten Geometrie eine Rolle, etwa bei der Klassifizierung der Isometrien in Dimension 2 und 3 oder bei der Untersuchung von Bandornamentgruppen.
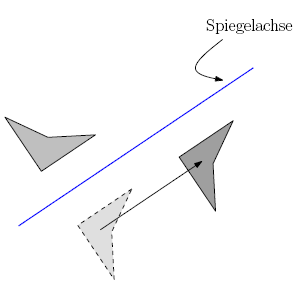
Gleitspiegelung
Beispiel
In der zweidimensionalen Geometrie ist eine Gleitspiegelung eine Spiegelung an einer Geraden verknüpft mit einer Translation parallel zu dieser Geraden:
Isometrien in euklidischen Vektorräumen der Dimension 2 können nach geometrischen Gesichtspunkten klassifiziert werden. Innerhalb dieser Klassifikation ist die Gleitspiegelung eine von insgesamt 5 Typen.
Scherzhafte Beispiele haben manchmal größere Bedeutung als ernste.
Michael Stifel
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Gleitspiegelung
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе