Das reguläre Fünfeck

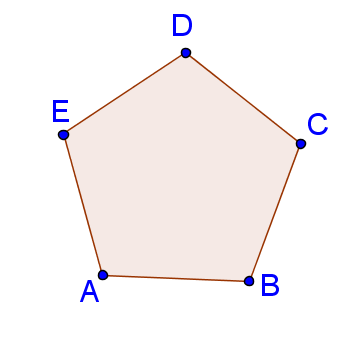
5e.png
Abb. 1: Bezeichnungen am Fünfeck.
Ein reguläres Polygon mit fünf Eckpunkten heißt reguläres Fünfeck oder einfach Fünfeck, wenn keine Verwechslungen mit nichtregulären Fünfecken zu befürchten sind.
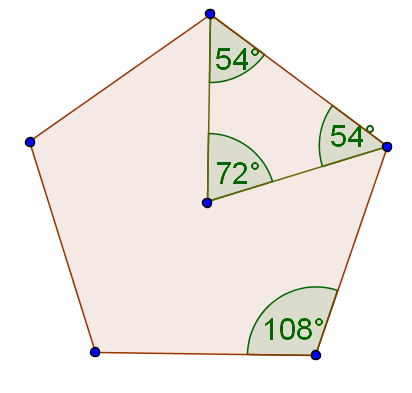
5eWi.png
Abb. 2: Winkel am Fünfeck.

Formeln

Winkel

Die Summe der Innenwinkel eines Fünfecks beträgt stets 540°540° und ergibt sich aus einer allgemeinen Formel für konvexe Polygone (Satz C7PF):
∑α=(n−2)⋅180∘=3⋅180∘=540∘ \sum\limits {\alpha =}(n - 2) \cdot 180^\circ = 3 \cdot 180^\circ = 540^\circ.
Der Innenwinkel - also der Winkel, den zwei benachbarte Seitenkanten miteinander einschließen - beträgt α=540°5\alpha=\dfrac{540°} 5, also
α=108∘ \alpha = 108^\circ.
Bildet man ausgehend vom Mittelpunkt Dreiecke wie in Abb. 2, so haben diese gleichschenkligen Dreiecke die dort angegeben Innenwinkel.

Flächeninhalt

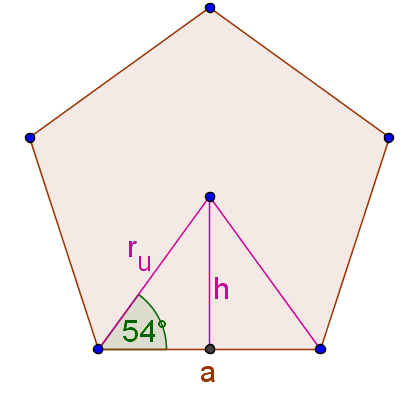
5eFl.png
Abb. 3: Zur Bestimmung des Flächeninhalts des Fünfecks.
Wir zerlegen das Fünfeck in 5 kongruente Teildreiecke (vgl Abb. 3). Für ein Teildreieck gilt: tan⁡54°=ha/2\tan 54°=\dfrac h { a /2}, also h=a2tan⁡54°h=\dfrac a 2\tan 54°, für die Dreiecksfläche ergibt sich AD=12a2tan⁡54°A_D=\dfrac {1} 2 a^2\tan 54° und für das Fünfeck damit:
A=54⋅a2⋅tan⁡54∘ ≈ 1,7204774⋅a2A= \dfrac{5}{4} \cdot a^2 \cdot \tan 54^\circ \,\approx\, \text{1,7204774}\cdot a^2

Umkreis

Es gilt (siehe Abb. 3): cos⁡54°=a/2ru\cos 54°=\dfrac {a/ 2} {r_u} und damit haben wir folgen Zusammenhang zwischen Umkreisradius und Seitenlänge:
a=2⋅ru⋅cos⁡54∘a=2 \cdot r_u \cdot \cos 54^\circ,
oder auch:
a=ru⋅5−52≈1,1755705⋅rua=r_u \cdot \sqrt{\dfrac{5 - \sqrt{5}}{2}} \approx 1,1755705\cdot r_u .
5ePenta.png
Abb. 4: Fünfeck und Pentagramm

Das Pentagramm

Die Diagonalen des Fünfecks bilden das Pentagramm - einen fünfzackigen Stern. In dessen Inneren befindet sich ein - um 180° gedrehtes - regelmäßiges Fünfeck. Diesem könnte man wieder ein Pentagramm einbeschreiben und so fort.
Der spitze Winkel im Zacken des Pentagramms beträgt 36°36°, also ein Drittel des 108°108° großen Innenwinkels des Fünfecks. Diese einfachen Winkelverhältnisse führen zu reizvollen geometrischen Kombinationen von Fünfecken und Pentagrammen.
 
 

Jede Wissenschaft bedarf der Mathematik, die Mathematik bedarf keiner.

Jakob I. Bernoulli

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie