Konstruktion eines regelmäßigen Fünfecks mit Zirkel und Lineal

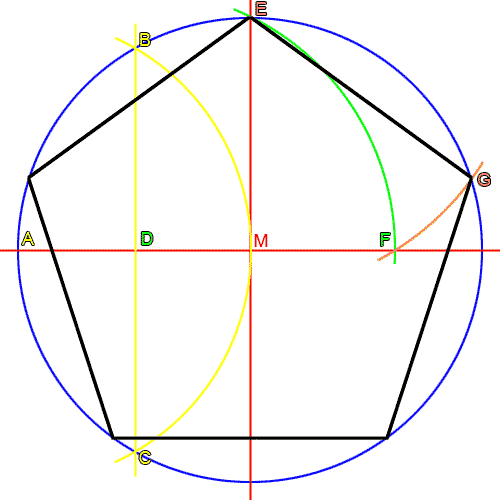
1. Einen blauen Kreis mit beliebigem Radius r um den Mittelpunkt M zeichnen und die roten Mittelsenkrechten einzeichnen.
2. Ein Schnittpunkt jeder Mittelsenkrechten mit dem Kreis wird mit A bzw. E bezeichnet.
3. Mit dem selben Radius r um A einen weiteren gelben Kreis zeichnen, der den blauen Kreis zweifach schneidet.
4. Die Schnittpunkte der beiden Kreise ergeben die Punkte B und C.
5. Die gelbe Gerade BC einzeichnen, sie schneidet die Strecke AM genau in der Hälfte im Punkt D.
6. Den grünen Kreis mit dem Radius $\overline {DE}$ um D zeichnen. Er schneidet die rote Gerade $\overline {AM}$ im Punkt F.
7. Der orange Kreis mit Radius $\overline {EF}$ um E schneidet den blauen Kreis in G (und im genau gegenüberliegenden Punkt J, der hier nicht eingezeichnet ist).
8. Mit zwei weiteren Kreisen um die Punkte G und J können die nicht eingezeichneten fehlenden Eckpunkte H und I konstruiert werden.

Es ist unmöglich, die Schönheiten der Naturgesetze angemessen zu vermitteln, wenn jemand die Mathematik nicht versteht. Ich bedaure das, aber es ist wohl so.

Richard Feynman

Polygone

• Reguläre Polygone
• Fünfeck
  • Konstruktion
• Sechseck
• Siebeneck
• Achteck
• Neuneck
• Siebzehneck