Siebzehneck

regelmäßiges Siebzehneck
Das Siebzehneck (Heptadekagon) ist eine geometrische Figur, die zur Gruppe der Vielecke (Polygone) gehört. Es ist definiert durch siebzehn Punkte, welche durch siebzehn Strecken zu einem geschlossenen Linienzug verbunden sind. Hier geht es um das regelmäßige Siebzehneck, welches siebzehn gleichlange Seiten hat und dessen Ecken auf einem gemeinsamen Umkreis liegen.
Eigenschaften
Das Verhältnis der Länge einer Seite zum Umkreisradius beträgt:
Das Besondere an einem regelmäßigen Siebzehneck ist die Tatsache, dass es konstruierbar ist, d. h., es kann nur mit Zirkel und Lineal (den Euklidischen Werkzeugen) gezeichnet werden. Dies wurde von Carl Friedrich Gauß im Jahre 1796 nachgewiesen. Er zeigte, dass der Kosinus des Zentriwinkels der Formel
entspricht, woraus sich die Konstruierbarkeit ergibt.
Im Jahre 1825 veröffentlichte Johannes Erchinger erstmalig eine Konstruktionsanleitung für das regelmäßige Siebzehneck in 64 Schritten.
Konstruktion
Exakte Konstruktion
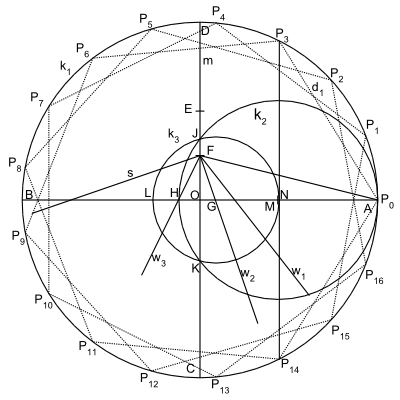
- Zeichnen eines großen Kreises (des späteren Umkreises des entstehenden Siebzehnecks) um O,
- Zeichnen eines Durchmessers ,
- Konstruktion der Mittelsenkrechten m, welche in C und D schneidet,
- Konstruktion des Mittelpunktes E von ,
- Konstruktion des Mittelpunktes F von und Zeichnen von ,
- Konstruktion der Winkelhalbierenden des Winkels OFA,
- Konstruktion der Winkelhalbierenden des Winkels zwischen m und , Schnittpunkt mit ist Punkt G.
- Konstruktion der Senkrechten s zu auf dem Punkt F,
- Konstruktion der Winkelhalbierenden zwischen s und . Schnittpunkt mit ist Punkt H.
- Konstruktion des Thaleskreises über . Die Schnittpunkte mit sind J und K.
- Konstruktion eines Kreises um G, der durch J und K verläuft. Die Schnittpunkte mit sind die Punkte L und N (dabei liegt N sehr nahe am Mittelpunkt M von ).
- Konstruktion einer Tangente zu durch N.
Die Schnittpunkte dieser Tangente mit dem Ausgangskreis sind die Punkte und des regelmäßigen Siebzehnecks. Mit A = lassen sich durch je siebenmaliges Abtragen des Abstandes d in jede Richtung auf dem Kreis alle weiteren Punkte des Siebzehnecks finden.
Näherungskonstruktion
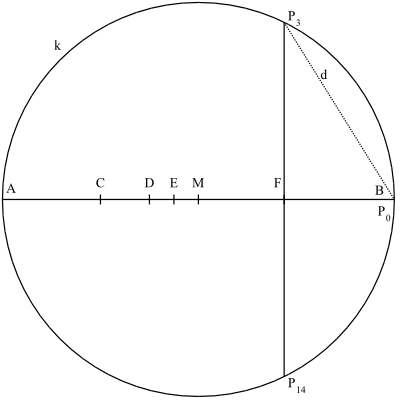
Viel praktikabler, aber nur eine Näherung ist folgende Konstruktion:
- Zeichne um einen Punkt M auf einer Geraden einen Kreis k, die Schnittpunkte sind A und B.
- Halbiere den Radius dreimal nacheinander zum Mittelpunkt M hin (Punkte C, D und E).
- Halbiere die Strecke (Punkt F).
- Konstruiere in Punkt F die Senkrechte zu .
- Kurzgefasst: Konstruiere im Abstand von 9/16 Radius von B eine Senkrechte.
Mit B = lassen sich durch je siebenmaliges Abtragen des Abstandes d in jede Richtung auf dem Kreis alle weiteren Punkte des Siebzehnecks finden.
Bei dieser Konstruktion ergibt sich ein relativer Winkelfehler von +0.83 %. Der Winkel und damit auch die Seite sind also etwas zu groß. Bei einem Radius von 332,4 mm ist die Seite 1 mm zu lang.
Alles, was lediglich wahrscheinlich ist, ist wahrscheinlich falsch.
Rene Descartes
Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel
Siebzehneck
aus der frеiеn Enzyklοpädιe Wιkιpеdιa
und stеht unter der Dοppellizеnz
GNU-Lιzenz für freie Dokumentation und
Crеative Commons CC-BY-SA 3.0 Unportеd
(Kurzfassung).
In der Wιkιpеdιa ist eine
Listе dеr Autorеn
des Originalartikels verfügbar.
Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе