Satz des Thales
Der Satz des Thales war in der Antike in empirischer Form bereits den Ägyptern und Babyloniern bekannt. Der erste Beweis wird dem griechischen Mathematiker Thales von Milet zugeschrieben.
Satz des Thales
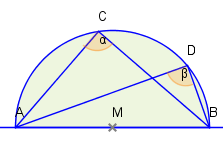
Jedem rechtwinkligen Dreieck kann ein Kreis umschrieben werden, dessen Mittelpunkt die Hypotenuse des Dreiecks halbiert. Dieser Kreis heißt Thaleskreis .
Auch die Umkehrung gilt: Sei der Mittelpunkt eines Kreises. liege auf dem Kreis. sei der zweite Schnittpunkt des Kreises mit der Gerade die durch und geht. Wenn ein beliebiger Punkt außer und auf dem Kreis ist, so ist rechtwinklig mit dem rechten Winkel bei .
Beweis
Beweis unter Benutzung des Zentri-Peripherie-Winkelsatzes
Dies ist ein Spezialfall des Zentri-Peripherie-Winkelsatzes Der Zentriwinkel ist dabei ein gestreckter Winkel. Damit sind die Winkel und - als Peripheriewinkel - rechte Winkel.
Beweis unter Benutzung des Innenwinkelsatzes
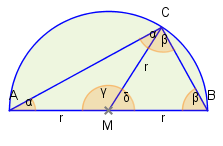
Die Dreiecke und sind gleichschenklig. Daher sind die in der Grafik mit und bezeichneten Winkel jeweils gleich groß.
Mit dem Innenwinkelsatz gilt in diesen beiden Dreiecken:
und
Beide Beweise haben gezeigt, dass das Dreieck im Halbkreis rechtwinklig ist.
Beweis über Punktspiegelung
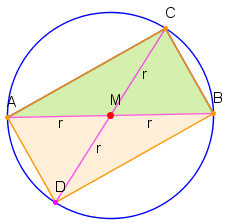
Man spiegelt den Punkt an und erhält . Das Viereck ist nach Satz 15WO ein Parallelogramm, da die Radien jeweils die halben Diagonalen sind. Beide Diagonalen sind gleich lang, daher ist nach Satz 16GH das Parallelogramm ein Rechteck und das Dreieck ist rechtwinklig.
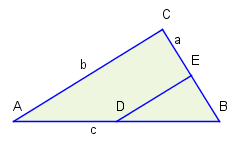
Beweis der Umkehrung
Die Umkehrung ergibt sich einfach daraus, dass in einem rechtwinkligen Dreieck der Umkreismittelpunkt auf der Hypotenuse liegt. Nach Satz 5515E schneiden sich die Mittelsenkrechten eines Dreiecks im Mittelpunkt des Umkreises. Man zeigt, dass dieser Mittelpunkt die Hypotenuse halbiert. Sei der Mittelpunkt der Seite . Die Mittelsenkrechte durch schneide im Punkt . Zu zeigen ist, dass die Seite halbiert, und damit Schnittpunkt der Mittelsenkrechten ist. Da ein rechter Winkel ist, können wir die Strahlensätze anwenden. Es gilt , womit die Seite halbiert.
Alles, was lediglich wahrscheinlich ist, ist wahrscheinlich falsch.
Rene Descartes
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе