Das Parallelogramm

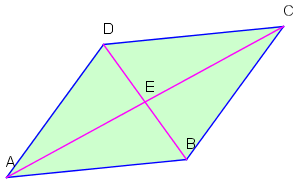
para.png
Ein Viereck mit zwei paarweise parallelen Seiten wird Parallelogramm genannt. Nach Definition ist jedes Parallelogramm ein Trapez.
In der Abbildung sind die Seiten AB‾\overline{AB} und CD‾\overline{CD} sowie AD‾\overline{AD} und BC‾\overline{BC} parallel.
Die gegenüberliegenden Innenwinkel sind gleich; sie sind Wechselwinkel an den parallelen Seiten. Die benachbarten Winkel ergänzen sich zu 180°. (Sie sind Nebenwinkel.)
 
 

Satz 16GF (Charakterisierung des Parallelogramms)

  1. Ein Viereck ist genau dann ein Parallelogramm, wenn gegenüberliegende Seiten gleich lang sind.
  2. Ein Viereck ist genau dann ein Parallelogramm, wenn sich seine Diagonalen halbieren.

Beweis

(1) AB∣∣CDAB||CD und AD∣∣BCAD||BC
  ⟺   ∣AB∣∣CD∣=∣BE∣∣DE∣=∣AE∣∣CE∣\iff \, \dfrac {|AB|}{|CD|}=\dfrac {|BE|}{|DE|}=\dfrac {|AE|}{|CE|} und ∣BC∣∣AD∣=∣BE∣∣DE∣=∣CE∣∣AE∣\dfrac {|BC|}{|AD|}=\dfrac {|BE|}{|DE|}=\dfrac {|CE|}{|AE|} (Strahlensätze)
Nun ist ∣AE∣∣CE∣=∣CE∣∣AE∣  ⟺  ∣AE∣=∣CE∣\dfrac {|AE|}{|CE|}=\dfrac {|CE|}{|AE|}\iff |AE|=|CE|, daher gilt
∣AB∣=∣CD∣|AB|=|CD| und ∣AD∣=∣BC∣|AD|=|BC|. Bei der Umkehrung benutzt man im letzten Schritt des Beweises die Umkehrung der Strahlensätze um auf die Parallelität AB∣∣CDAB||CD und AD∣∣BCAD||BC zu schließen. □\qed
(2) Der Beweis des zweiten Teils ist schon im ersten Teil enthalten. Der folgende Beweis kommt ohne Strahlensatz aus und benutzt Kongruenzen von Dreiecken.
"  ⟹  \implies": Wenn EE der Schnittpunkt der Diagonalen ist, dann sind die Dreiecke ΔABE\Delta ABE und ΔDEC\Delta DEC kongruent. Sie stimmen in einer Seite (AB‾\overline{AB} bzw. CD‾\overline{CD}) und zwei anliegenden Winkeln (welche man als Wechselwinkel wiederfinden kann) überein. Damit gilt: ∣BE‾∣=∣ED‾∣|\overline{BE}|=|\overline{ED}|. Durch einen analogen Schluss bei den anderen Teildreiecken ergibt sich die Behauptung.
"⇐\Leftarrow": Seien nun in einem beliebigen Viereck die Diagonalenhälften gleich lang. Dann sind die Dreiecke ABEABE und CDECDE kongruent (zwei Seiten und eingeschlossener Winkel als Scheitelwinkel). Gleiches gilt für die Dreiecke AEDAED und BECBEC. Daher gilt ∣AB∣=∣CD∣|AB|=|CD| und ∣AD∣=∣BC∣|AD|=|BC| und nach Satz 16GF handelt es sich um ein Parallelogramm. □\qed

Gott existiert, weil die Mathematik widerspruchsfrei ist, und der Teufel existiert, weil wir das nicht beweisen können.

Andre Weil

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Planimetrie