Stufenwinkel und Wechselwinkel

Stufenwinkel

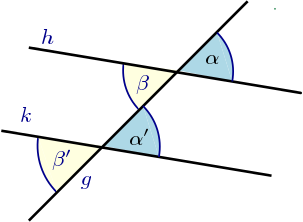
StuWi.png
Abb. 1: Stufenwinkel an geschnittenen Parallelen
Wenn zwei parallele Geraden h∣∣kh||k von einer dritten Geraden gg in den Punkten AA und BB geschnitten werden, ergeben sich an diesen Scheitelpunkten Paare von Nebenwinkeln und Scheitelwinkeln.
Die Winkel α\displaystyle{\alpha} und α′\displaystyle{\alpha'} heißen Stufenwinkel (ebenso β\beta und β′\beta').
Da die Geraden hh und kk durch eine Verschiebung ineinander überführt werden können, gilt α=α′\alpha=\alpha', β=β′\beta=\beta'.
Die aus Gründen der Übersichtlichkeit in Abb. 1 nicht eingezeichneten Winkel bilden ebenfalls Paare von Stufenwinkeln, die gleich groß sind.

Wechselwinkel

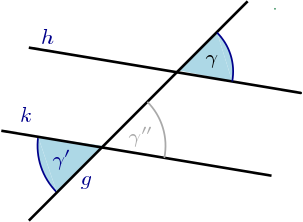
WeWi.png
Abb. 2: Wechselwinkel an geschnittenen Parallelen
Die Winkel γ\gamma und γ′\gamma' heißen Wechselwinkel (ebenso die anderen entsprechenden Winkel).
Sie sind gleich, da γ\displaystyle{\gamma} und γ′′\displaystyle{\gamma{''}} Scheitelwinkel sind und γ′′\displaystyle{\gamma{''}} und γ\displaystyle{\gamma} wiederum Stufenwinkel.

Satz 5515B (Stufenwinkelsatz und Wechselwinkelsatz)

Seien h\displaystyle{{h}} und k\displaystyle{{k}} zwei parallele Geraden, die von einer Geraden gg geschnitten werden. Dann gilt:
  1. Die Stufenwinkel aus Abb. 1 sind gleich (α=α′\alpha=\alpha', β=β′\beta=\beta').
  2. Die Wechselwinkel aus Abb. 2 sind gleich (γ=γ′\gamma = \gamma').

Umkehrung des Stufenwinkelsatzes

Auch die Umkehrung des Stufenwinkelsatzes gilt. Sind Stufenwinkel an Geraden gleich groß, so sind diese Geraden parallel.
Den Beweis kann man indirekt führen.
Auch die Umkehrung des Wechselwinkelsatzes ist gültig.
 
 

Seit der Zeit der Griechen bedeutet "Mathematik" zu sagen, "Beweis" zu sagen.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Grundbegriffe