Nebenwinkel und Scheitelwinkel

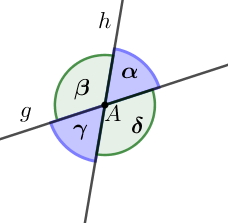
WinkelGeraden.png
Zwei sich schneidende Geraden gg und hh ergeben am Schnittpunkt AA vier Winkel α\alpha, β\beta, γ\gamma und δ\delta. Die Winkel α\alpha und β\beta heißen Nebenwinkel (ebenso die Winkel β\beta und γ\gamma; γ\gamma und δ\delta; δ\delta und α\alpha). Die Winkel α\alpha und γ\gamma heißen Scheitelwinkel (ebenso die Winkel β\beta und δ\delta).
Für diese Arten von Winkel gelten folgende Eigenschaften:

Satz 5515A (Nebenwinkel und Scheitelwinkel)

  1. Nebenwinkel ergänzen sich zu 180°; also α+β=γ+δ=180°\alpha+\beta=\gamma+\delta=180°.
  2. Scheitelwinkel sind gleichgroß; also α=γ\alpha=\gamma und β=δ\beta=\delta.

Beweis

(i) Der erste Teil der Behauptung ergibt sich unmittelbar daraus, dass die Winkel α\alpha und β\beta zusammen einen gestreckten Winkel (der durch die Gerade hh gebildet wird) ergeben. Analoges gilt für die anderen Winkelkombinationen.
Aus (i) wissen wir, dass α+β=180°\alpha+\beta=180° und β+γ=180°\beta+\gamma=180° gilt. Subtrahieren wir diese beiden Gleichungen voneinander, erhalten wir α−γ=0\alpha-\gamma=0, also α=γ\alpha=\gamma. □\qed
 
 

Strukturen sind die Waffen der Mathematiker.

N. Bourbaki

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Grundbegriffe